Type I-III 平方和
Type I-III 平方和
平方和(Sum of Squares, SS)在统计学中是一个非常核心的概念,主要用于衡量数据相对于某个基准(通常是平均数)的离散程度。
基本定义
在统计学中,我们关心与某个值的差异的平方和。于是就有了:
- 离均差平方和 (Sum of Squares about the Mean) :\sum_{i=1}^n (x_i - \bar{x})^2这是样本方差和标准差的核心。
- 总平方和、回归平方和、残差平方和等是这个基本思想的延伸。
常见形式
在统计学中,平方和有不同的形式,取决于参考点是谁:
- 总平方和 (Total Sum of Squares, SST) 衡量数据相对于总体均值的总变异。SST = \sum_{i=1}^n (y_i - \bar{y})^2这里 y_i 是观测值,\bar{y} 是样本均值。
- 回归平方和 (Regression Sum of Squares, SSR 或 SSM) 衡量模型预测值相对于总体均值的变异。SSR = \sum_{i=1}^n (\hat{y}_i - \bar{y})^2
- 残差平方和 (Error Sum of Squares, SSE)
衡量观测值相对于模型预测值的误差大小。
SSE = \sum_{i=1}^n (y_i - \hat{y}_i)^2
并且它们满足分解关系:
SST = SSR + SSE
如何把“可解释的变异”(SSR)分配给不同自变量
理解 ANOVA 中的平方和类型:Type I、Type II 与 Type III
在统计学研究中,ANOVA(方差分析)是用来检验不同因素及其交互作用对因变量影响的常用方法。然而,当数据出现 不平衡设计(unbalanced design) 时,即不同实验组的样本数量不一致,研究者必须面对一个核心问题:如何划分和解释平方和(sums of squares, SS) 。
为什么会有不同的平方和?
在 平衡设计 下(各组样本数相等),三种方法结果一致。但在现实中,几乎所有调查和实验都会产生不平衡:比如有的组别招募到的人多,有的少。此时,如何处理“组间不均衡”就成了关键。
统计学家从 1930 年代起(Yates, 1934)就开始提出不同的解决办法,这些方法后来被软件实现并命名为 Type I、Type II、Type III。
三种平方和方法详解
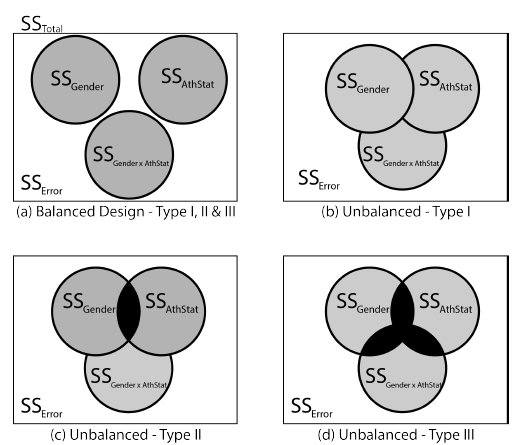
摘自Smith & Cribbie (2014)
🔹 Type I 平方和
-
原理:逐步引入因素,先进入的因素不受其他因素调整,后进入的因素在控制前面因素的条件下检验。
-
特点:
- 结果依赖于因素进入的顺序。
- 如果换顺序,结果可能完全不同。
-
优点:
- 在模型构建阶段有用,可以探索不同因素顺序下的效应。
-
局限:
- 很少用于最终推断,因为缺乏统一性。除非研究者有明确的理论顺序,否则不推荐。
🔹 Type II 平方和
-
原理:
- 主效应在控制其他主效应的情况下检验,但不控制交互作用。
- 例如,检验性别效应时会控制运动员身份,但不考虑性别 × 身份交互。
-
特点:
- 遵循 边际性原则(marginality principle) ,避免在交互作用存在时错误解读主效应。
- 如果交互作用不显著,Type II 在统计效能上优于 Type III。
-
学界评价:
- Smith & Cribbie (2022)推荐 Type II 作为默认选择,因为它逻辑一致、统计效力高。
- Langsrud (2003)认为 Type II 是比 Type III 更“现实”的检验方式,因为 Type III 往往基于不合理的模型假设。
-
适用情境:
- 当没有显著交互作用时,应首选 Type II。
🔹 Type III 平方和
-
原理:
- 主效应在控制所有其他主效应和交互作用的情况下检验。
- 其检验的是各组 等权平均值 是否相等。(即每组的权重相等,而不是按照各组人数来建立权重)
-
特点:
- 是 SPSS、SAS 等软件的默认方法。
- 不依赖样本量比例,而是看“每组是否等权”。
-
优点:
- 在没有假设前提时比较“安全”,因为不需要假设交互作用不存在。
- 检验假设更直观:例如“各水平的均值相等”。
-
局限:
- 违反边际性原则:在存在交互作用时解读主效应毫无意义(Nelder, 1994)。
- 在很多不平衡设计下,其统计效力明显低于 Type II。
学界争论与应用案例
-
Type III 的批评:
- Nelder 和 Lane(1995)指出,Type III 实际上是在检验“不存在主效应但存在交互作用”的模型,这种模型通常是 不现实的。
- Kempthorne(1975) 提出了更加犀利的批评:“在没有额外信息的情况下,交互作用存在时检验主效应是荒谬的。The testing of main effects in the presence of interaction, without additional input, is an exercise in fatuity. ”
-
Type II 的优势:
- 多项模拟研究表明,在没有显著交互作用时,Type II 拥有更高的统计功效(power)(Lewsey and Gardiner et al., 2001)(Monette and Fox, 2009)。
- 在临床试验中,Type II 常被推荐。Senn (1998) 指出,在多中心试验中,Type III 甚至可能得出“多信息反而更差”的悖论,而 Type II 表现更稳健。
-
Type I 的特殊角色:
- 尽管不适合最终结论,但在 模型探索和构建阶段,顺序检验可以帮助研究者发现潜在模式。
- 因此,Type I 常被视为“辅助工具”,而非主要检验方法。
如何选择?实用指南
-
先检验交互作用:
- 如果交互作用显著 → 不要解读主效应,而应直接分析交互作用(如简单效应或交互对比)。
-
如果交互作用不显著:
- 优先使用 Type II:逻辑严谨,统计效能更高。
- 谨慎使用 Type III:仅在你确实需要检验“等权均值差异”时。
- Type I 只在模型探索或有强理论顺序时考虑。
-
一句话总结:
- 推荐:Type II > Type III > Type I(仅限特殊情况) 。
结语
Type I、II、III 平方和的争论已持续近百年。总体而言:
- Type I:顺序敏感,更像探索工具。
- Type II:更符合统计逻辑,适合作为默认选择。
- Type III:虽然软件常用,但在很多情况下逻辑上站不住脚。
如 Smith & Cribbie (2014) 总结的那样:
“Type III 只有在最不该解释主效应的时候才显得合理。”
因此,研究者应打破“跟着软件默认走”的习惯,更加主动地选择最合适的平方和方法。
参考文献
Kempthorne, O. (1975). Fixed and Mixed Models in the Analysis of Variance. Biometrics, 31(2), 473–486. https://doi.org/10.2307/2529432
Langsrud, Ø. (2003). ANOVA for unbalanced data: Use Type II instead of Type III sums of squares. Statistics and Computing, 13(2), 163–167. https://doi.org/10.1023/A:1023260610025
Lewsey, J. D., Gardiner, W. P., & Gettinby, G. (2001). A Study of Type Ii and Type Iii Power for Testing Hypotheses from Unbalanced Factorial Designs. Communications in Statistics - Simulation and Computation, 30(3), 597–609. https://doi.org/10.1081/SAC-100105081
Monette, G., & Fox, J. (2009). A Framework for Hypothesis Tests in Statistical Models With Linear Predictors.
Nelder, J. A., & Lane, P. W. (1995). The Computer Analysis of Factorial Experiments: In Memoriam-Frank Yates. The American Statistician, 49(4), 382–385. https://doi.org/10.2307/2684580
Senn, S. (1998). Some controversies in planning and analysing multi-centre trials. Statistics in Medicine, 17(15–16), 1753–1765; discussion 1799-1800. https://doi.org/10.1002/(sici)1097-0258(19980815/30)17:15/161753::aid-sim9773.0.co;2-x
Smith, C. E., & Cribbie, R. (2022). Factorial ANOVA with Unbalanced Data: A Fresh Look at the Types of Sums of Squares. Journal of Data Science, 12(3), 385–404. https://doi.org/10.6339/JDS.201407_12(3).0001
Yates, F. (1934). The Analysis of Multiple Classifications with Unequal Numbers in the Different Classes. Journal of the American Statistical Association, 29(185), 51–66. https://doi.org/10.1080/01621459.1934.10502686
