花卷铺

花卷铺

LGCM

计量
26
2025-12-21

LGCM

Chapter 7 Linear LGCM

描述随时间的系统性变化

捕捉个体间差异：初始水平（截距）与变化速度（斜率）

连续观测变量

一般形式

y_{ti} = \beta_{0i} + \beta_{1i} x_{ti} + r_{ti} \quad (7.1)

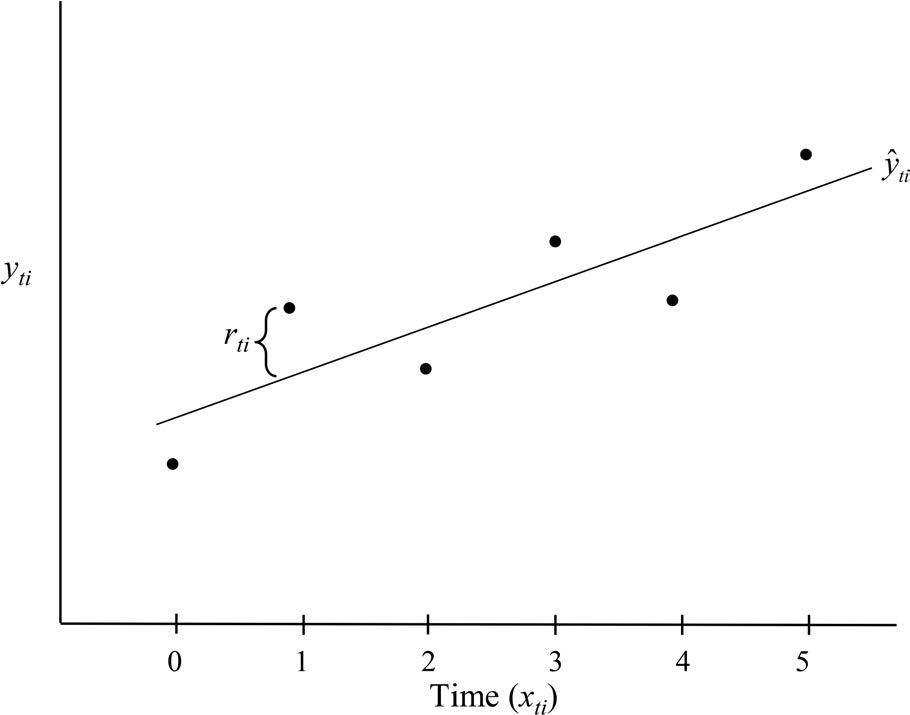
​\;r_{i i}=y_{i i}-{\hat{y}}_{i i} 在个体内时一般被称为个体内方差

\beta_{0i}=\gamma_{00}+u_{0i} \quad (7.2)
\beta_{1i}=\gamma_{10}+u_{1i}\quad(7.3)

将 7.2 和 7.3 带入 7.1

\begin{array}{c}{{y_{ti}=\left(\gamma_{_{00}}+u_{_{0i}}\right)+\left(\gamma_{10}+u_{1i}\right)x_{ti}+r_{ti}}}\\ {{y_{ti}=\gamma_{00}+\gamma_{10}x_{ti}+u_{1i}x_{ti}+u_{0i}+r_{ti}}}\end{array}

该最终方程可视为线性回归模型，其右侧前两项构成标准线性回归结构，其余项则代表三个误差分量，而非单一误差项。此即应用于纵向数据的多层回归模型，其中时间点嵌套于个案内。​u_{0i} 表示任意个案截距值与样本平均截距的偏离程度，​r_{ti} 残差的方差常被称为个体内变异，​u_{0i} 残差的方差则反映个体间差异。​u_{1i} 残差提供了个体变化差异的信息，即任意个案斜率与平均斜率的偏离程度。

Latent Growth Curve Model, LGCM

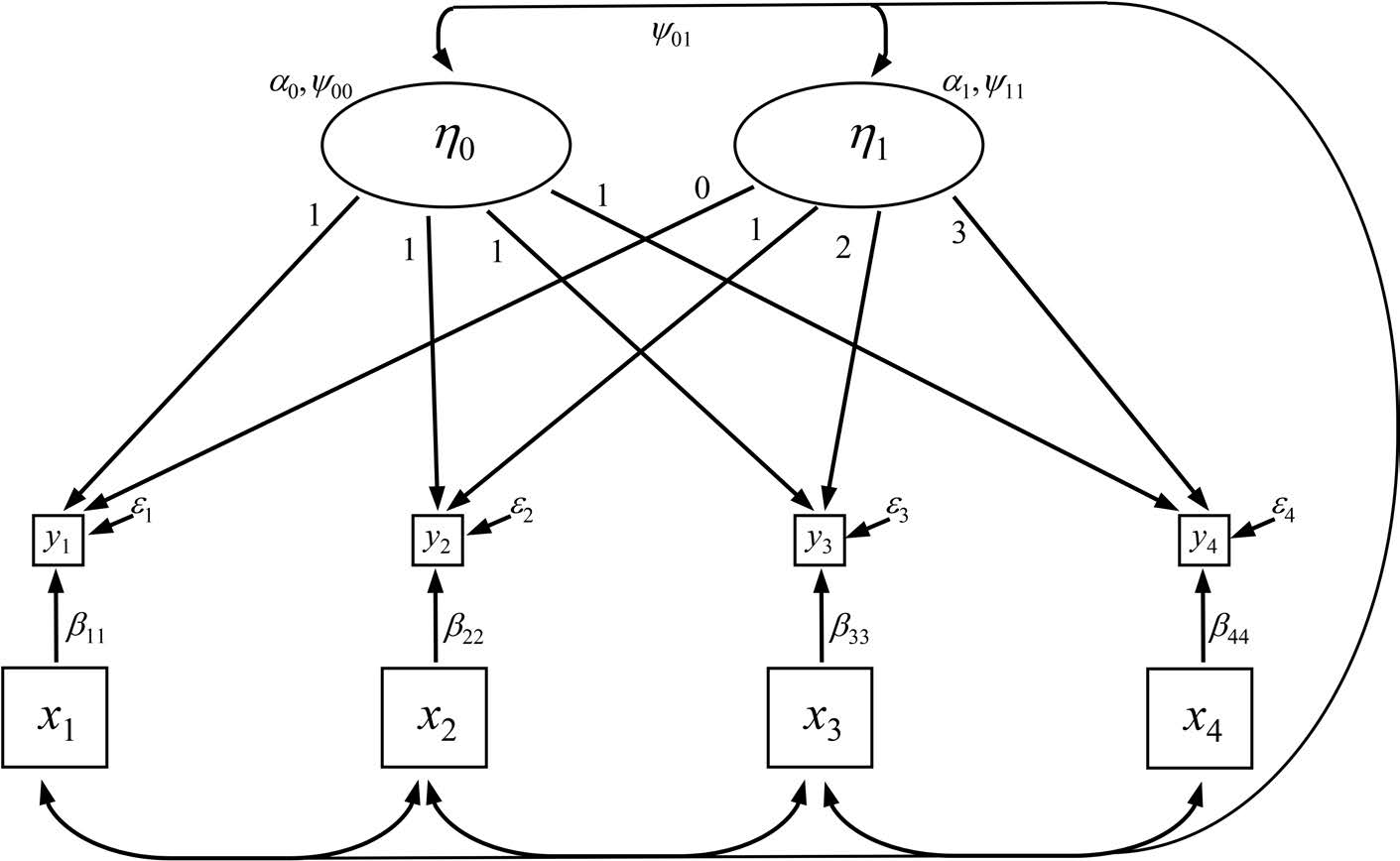
结构方程模型可通过在模型的测量部分施加特定约束，构建与多水平回归增长曲线分析中两组方程并行的方程组。案例层面的回归通过设定两个潜变量进行建模：一个潜变量 ​\eta_{0i} 代表截距，另一个潜变量 ​\eta_{1i} 代表斜率。

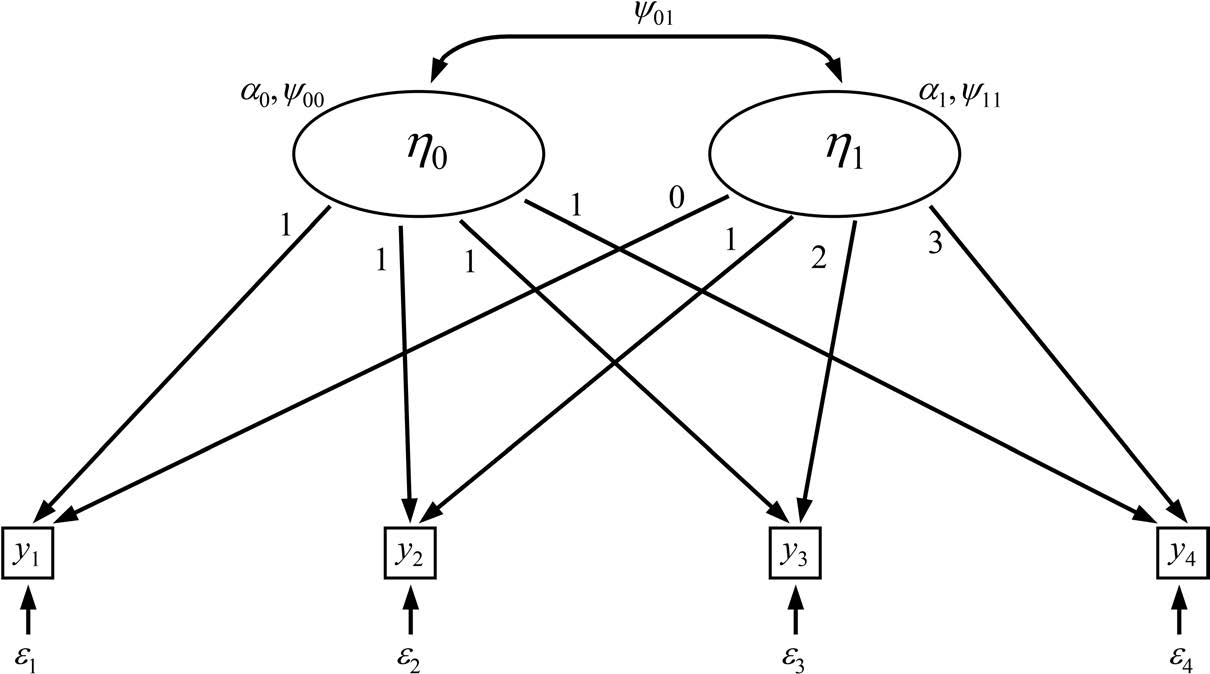
y_{i}=\lambda_{t0}\eta_{0i}+\lambda_{t1}\eta_{1i}+\varepsilon_{ti}

如果截距因子的载荷在所有时间点都设为 1，那么 ​\lambda_{t0} 就是一个常数，并且项 ​\lambda_{t0}\eta_{0i} 可简化为截距 ​\alpha_{0i}。

y_{ti} = \alpha_{0i} + \lambda_{t1}\eta_{1i} + \varepsilon_{ti}\quad (7.4)

当​\lambda_{ti}为时间时（比如 0,1,2,3 等）7.4 等同于 7.1，7.2 和 7.3 等价于下列 7.5 和 7.6

\eta_{0i}=\alpha_{0}+\zeta_{0i}\quad (7.5)
\eta_{1i}=\alpha_{1}+\zeta_{1i}\quad (7.6)

为了模型识别，将各个时间点的测量截距设置为 0，通过​Var(ζ_{0i}) = ψ_{00} and ​Var(ζ_{1i}) = ψ_{11}.来设定随机效应。然后将 7.5 和 7.6 带入 7.4,可得

\begin{aligned}y_{ti} &= (\alpha_{0}+\zeta_{0i})+\lambda_{t1}(\alpha_{1}+\zeta_{1i})+\varepsilon_{ti} \\y_{ti} &= \alpha_{0}+\alpha_{1}\lambda_{t1}+\zeta_{0i}+\zeta_{1i}\lambda_{t1}+\varepsilon_{ti}\end{aligned}\qquad (7.7)

最后三项 ​ζ_{0i} + ζ_{1i}λ_t + ε_{ti} 构成多水平方差成分，其中 ​Var(ζ_{0i}) = ψ_{00} 和 ​Var(ζ_{1i}) = ψ_{11} 反映个体间（第二水平）方差，​Var(ε_{ti}) = θ_{tti} 反映个体内（第一水平）方差。

该潜增长曲线模型可表述为通用结构方程形式：

​y_{ti} = η_{0i} + η_{1i}λ_t + ε_{ti}，

其中载荷为时间度量值（如 0, 1, 2, ..., T−1），截距因子与斜率因子的均值及方差需进行估计。

系数解释

平均斜率与斜率方差：趋势与个体差异

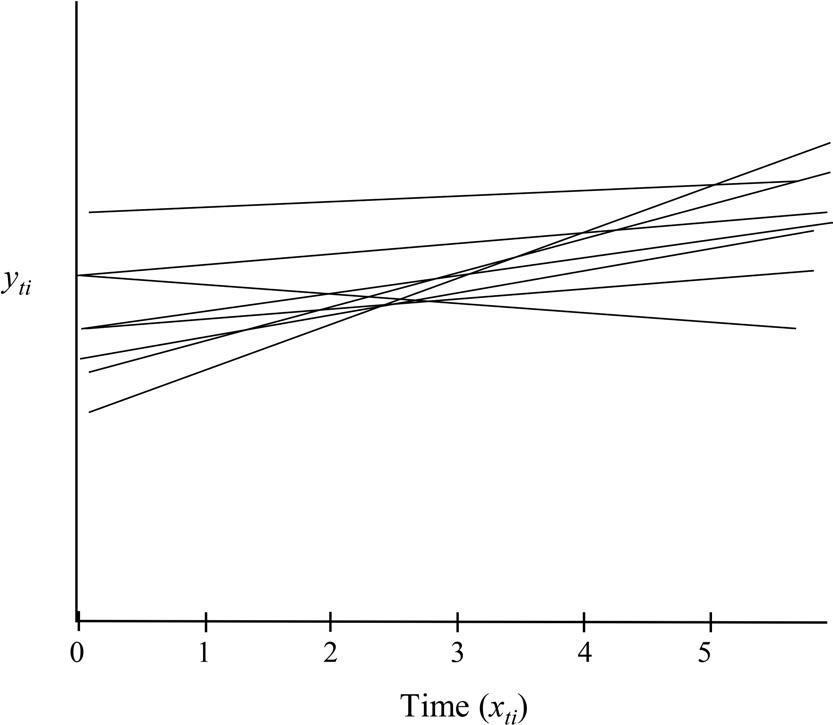
平均斜率 α₁ 表示样本平均随时间是上升或下降，其显著性检验与重复测量 ANOVA 的趋势检验等价。斜率方差 ψ₁₁ 表示个体间的增长差异，若显著，则表示个体的变化率不同、斜率不平行；若不显著，则说明个体在变化趋势上的差异不显著。增长模型比 ANOVA 能提供更多关于个体差异的信息。虽然斜率方差理论上很少为 0，但若为 0，表示所有人的变化曲线完全平行。

固定效应与随机效应：增长模型与多层模型的衔接

平均截距与平均斜率称为固定效应；截距方差与斜率方差称为随机效应，因为它们被假设在个体间随机变化。因此增长模型（广义的 GCM）也称为随机效应模型、随机系数模型或混合模型。除非遇到识别问题，模型很少把这些方差人为设为 0。

截距、斜率及协方差的显著性检验

一般较少关注截距方差的显著性，而更关注斜率方差是否显著。软件默认使用 Wald 检验（ψ/SEψ），也可用似然比检验，但后者在斜率方差的检验上有技术限制：若只检验斜率方差是否为 0，必须同时假设截距–斜率协方差为 0，否则模型为错设。因此可以选择（a）同时检验斜率方差 + 协方差（2 df），但无法分辨斜率方差本身是否显著；或（b）将斜率方差与协方差均设为 0，再释放斜率方差（1 df），但若真实协方差 ≠ 0，会导致模型错设。实证研究显示，样本量合理（如约 200）时 Wald 与 LRT 表现相近，因此实际应用中常采用 Wald 作为更简洁的解决方案。

截距–斜率相关的解释与模型意义

截距–斜率相关通常应估计。该相关反映个体初始水准与其随时间变化速度的关系：正相关表示基线越高，增长率越大（或下降越慢）；负相关则表示基线越高，增长率越小（或下降越快）。这一关系对解释个体差异至关重要。

四种典型情境：趋势方向 × 截距–斜率相关方向的组合解释

书中图 7.4 给出了四种示例，展示平均趋势（上升/下降）与截距–斜率相关（正/负）的不同组合如何改变解释：

  • 若平均趋势上升且相关为正，则初始高的人增长更快。
  • 若平均趋势上升但相关为负，则初始高的人增长更慢甚至下降。
  • 若平均趋势下降且相关为正，则初始高的人下降较慢甚至回升。
  • 若平均趋势下降且相关为负，则初始高的人下降更快。

这些情境有助于理解增长模型中个体差异的实际含义。

时间编码

将公式(7.4)参照回归方程解读

  • 截距即为当​x_{ti}等于 0 时​y_{ti}的期望值。
  • 若将​\eta_1的载荷设定为从 0 开始，则截距均值​\alpha_0可解释为第一个时间点​y_{ti}的期望值或样本平均值。
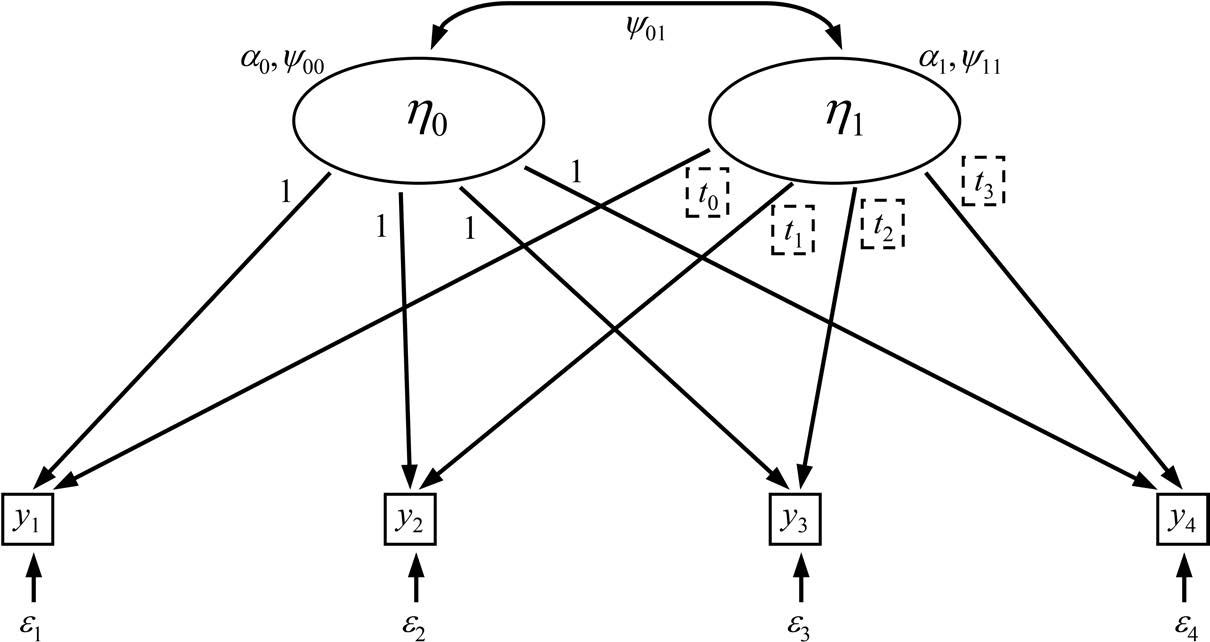
  • 替代编码方案还可适应不同测量时点的不等间距或非线性趋势。

假设采用单位为 1 的线性编码方案，改变斜率因子的载荷不会影响斜率因子均值的估计结果（与使用 0、1、2、…、T−1 时一致），然而截距会因编码方案的改变而变化，其方差也会受到影响。

与其他模型的关联

  • 若忽略斜率因子并仅设定具有单位载荷的单一"截距"因子，则该模型等同于第六章讨论的潜在状态-特质模型中的特质因子概念。
  • 若将潜在增长曲线模型设定为两个时间点，且斜率因子载荷分别设为 0 和 1，则该模型等价于第三章讨论的重复测量方差分析对比编码模型。
  • 增长曲线模型的优势在于：随着时间点数量的增加，随时间变化率的估计受特定时间点误差或时点特异性波动的影响会减小，从而能更可靠地估计水平变化。

增长模型斜率与差异分数分析之间的关系。

\beta_{1i}=\frac{y_{ti}-y_{t-1,i}}{x_{_{ti}}-x_{_{t-1,i}}}

如果是最传统的编码方式则分母值为 1，公式可简化为 ​\beta_{1i} = y_{ti} - y_{t-1,i}，即斜率为因变量的差值。

将平均斜率 α₁ 重新表述为两个均值之差

\alpha_1=E{\biggl(}y_{_{ti}}-y_{_{t-1,i}}{\biggr)}=E{\biggl(}y_{_{ti}}{\biggr)}-E{\biggl(}y_{_{t-1,i}}{\biggr)}

当时间是 0，1 编码时

\alpha_{1}=E\Big(y_{ti}\Big)-{\alpha}_{0} \quad (7.8)

即

E(y_{ti})=\alpha_0+\alpha_1

即第二个时间点的均值是平均斜率和平均截距之和，同理可以应用于多个时间点的情况。

不估计截距与斜率相关的潜在增长曲线模型，在数学上等同于一种特殊的 simplex model（自回归系数为 1、各时点扰动相等），这一模型形式与潜在变化分数模型也非常接近。由于自回归为 1 时两时点的回归等价于差分，因此这些模型之间的联系并不意外，而增长模型也可以在此基础上加入显式的自回归成分。

组内相关系数

仅含截距项且无增长因子的模型。ICC 表示组间方差占总方差的比例，其计算公式为截距因子方差​\text{Var}(\eta_0) = \Psi_{00}与总方差的比值。

\rho=\frac{\Psi_{00}}{\displaystyle{{Var}\!\left(y_{t i}\right)}}=\frac{\Psi_{00}}{\displaystyle\Psi_{{00}}+\theta_{{(tt)}}}

此处为便于分析，假定残差方差在各时间点上设置相等（Newsom, 2002），即存在单一残差值，满足 ​\text{Var}(\varepsilon_{ti}) = \theta_{(tt)}。若不对残差方差施加等值约束，则可采用其中位数或几何平均数作为其他可能的处理方式。

ICC 表示总方差中个体间差异所占比例，与状态—特质模型中的方差分解概念相似；在包含增长因子的模型中亦可计算“条件 ICC”，表示在控制线性变化后，截距（如基线分数）的个体间差异在总体方差中所占的比例。

信度

不是心理测量学的信度(Kreft, 1997)，而是指截距和斜率估计的稳定性，信度越高，SE 越小 (Raudenbush, 1988)

\rho=\frac{\Psi_{00}}{\Psi_{_{00}}+\theta_{{(tt)}}/T}\qquad\left(7.10\right)

其中​Var(\eta_0) = \Psi_{00}且​Var(\varepsilon_{ti}) = \theta_{(tt)}，其与组内相关系数公式的唯一区别在于考虑了时间点数量​T。

对于增长模型来说

\rho_{_{R B}}={\frac{\Psi_{11}}{\Psi_{11}+\theta_{{(tt)}}/T}} \qquad\left(7.11\right)

斜率因子方差估计值 ​\text{Var}(\eta_1) = \Psi_{11} 被用于替代截距因子方差估计值。

结合截距方差​\psi_{00}、斜率方差​\psi_{11}及其协方差​\psi_{01}估计值的信度指数 (McArdle & Epstein, 1987)：

\rho_{M E}=\frac{\Psi_{00}+2\lambda_{\it t1}\Psi_{01}+\lambda_{\it t1}^{2}\Psi_{11}}{\Psi_{00}+2\lambda_{\it t1}\Psi_{01}+\lambda_{\it t1}^{2}\Psi_{11}+\theta_{(n)}}

Willett (1989)考虑时间度量间距的分布逻辑——自变量方差越大应能提升信度与统计检验力。将公式（7.11）的 ​T 替换为时间点离均差平方和 ​SST_{(tt)} = \sum (t - \bar{t})^2。

\rho_{W}=\frac{\Psi_{11}}{\Psi_{11}+\theta_{(tt)}/\,\!S S T} \qquad\left(7.12\right)

Brandmaier 等人 (2018) 提出了一个与 Willett 所提指标密切相关的信度指数——有效曲线信度，旨在提升检验力计算中的效应量估计精度，并改进跨研究信度比较

\rho_{_{ECR}}=\frac{\Psi_{{11}}}{\Psi_{{11}}+\theta_{{eff}}}

其中

\theta_{\mathrm{eff}}=\frac{\theta_{(tt)}}{\sum t^{2}-\left(\frac{1}{T+\frac{\theta_{(tt)}}{\psi_{00}}}\right)\left(\sum t\right)^{2}}

​\rho_{ECR} 的分母包含​\Psi_{00}（截距因子方差），因此当个体间变异性较小时，信度估计值更高。反之，分母是时间点数量与时间点离散度的函数，故类似于 Willett 指数中使用的 SST 值——时间点离散度增大时，信度会呈指数级增长。当截距因子与斜率因子无相关性且个体内方差为零（即 θ(tt) = 0）时，这两个信度指数相等。

Rast 与 Hofer（2014）的模拟研究比较了三种增长曲线斜率信度指标：​\rho_{ME}、​\rho_{W} 与 ​\rho_{RB}，发现 ​\rho_W（基于斜率变异）比 ​\rho_{ME} 更能反映检测变化差异的统计检验力。

在选择 ​\rho_W 或 ​\rho_{RB} 时，核心差异在于它们是否依赖真实时间间隔：

​\rho_{RB}：完全不考虑实际时间间隔，只看测量次数；无论访谈间隔是半年、1 年、2 年，甚至 10 年，只要波次一样，信度相同。

​\rho_{W}（及 ​\rho_{ECR} ）：强烈依赖真实时间间隔。时间平方和
​\mathrm{SST} = \sum (t_i - \bar{t})^2 越大， ​\rho_W 通常越大。若时间编码反映真实间隔（如双年访谈用 ​t = 0, 2, 4, 6 ），信度会明显上升。

这种做法基于一个隐含假设：更大的时间跨度能更容易检测到变化。Timmons & Preacher（2015）的模拟研究支持该观点（线性变化情境下：更多测量点 + 更大间隔 → 更高检验力）。

但 Collins & Graham（2002）指出，变化过程可分为缓慢与快速两种：

  • 慢速变化（slow change） ：如体重随年龄增长、幼儿社交技能 —— 较长间隔可能更适合。
  • 快速变化（rapid change） ：如情绪、消费信心 —— 较短间隔更能捕捉波动。

因此，虽然 ​\rho_W 随时间间隔扩大通常会上升，但 更长的实际间隔并不一定带来更高的测量精度；最佳间隔取决于所研究的变化速度与理论背景。

模型拟合

自由度

df = \frac{J(J+1)}{2} + J - q

观测变量数量为 ​J（在基础模型中等于 ​T），​q 为待估参数数量。

例：对于潜变量增长曲线模型，典型模型需估计截距因子方差 ​\psi_{00}、斜率因子方差 ​\psi_{11}、截距因子与斜率因子协方差 ​\psi_{01}、截距因子均值 ​\alpha_0、斜率因子均值 ​\alpha_1 以及各观测变量 ​J 的残差方差。

为识别因子均值，测量截距通常被约束为零，故不涉及额外参数。因此在此典型设定下，待估自由参数数量等于 5。

在潜在增长曲线模型（LGCM）中，因观测变量模型总是满足 ​J = T，自由参数数量 ​q = T + 5（Bollen & Curran, 2006）。因此要估计全部参数至少需要三个时间点。

若只有两个时间点，则需估计 ​T + 5 = 7 个参数，但可用的方差协方差元素只有​\frac{J(J+1)}{2} + 2 = \frac{2(3)}{2} + 2 = 5，因此必须施加约束（如在重复测量 ANOVA 中将残差方差设为 0）。

  • 在多水平模型中，软件默认假设残差方差随时间相等（可解除）；而在 SEM 中默认每个时间点的残差方差自由估计，因此异质性（方差不同）是默认设定。无论是哪种框架，都可以检验方差齐性：多水平模型常用 Bartlett 检验；LGCM 可通过比较残差方差自由与等值模型的似然比检验。允许残差随时间不同的模型通常拟合更好。
  • LGCM 的拟合取决于模型隐含协方差矩阵与真实协方差矩阵的差异。在线性增长模型中，缺乏拟合源自观测点偏离线性趋势，而残差方差反映多种来源：测量误差、时间点特有的系统性或随机变异、以及模型函数形式（如线性）的不正确性。因缺乏拟合可能来自多种因素，因此模型拟合不应自动视为函数形式是否正确，也不能用来判断斜率（增长量）的大小。例如：斜率为零但点均贴近水平线，则模型拟合极佳但无增长。
  • 常用拟合指标（SRMR、RMSEA、CFI）在 LGCM 中表现不一致。SRMR 对于时间点少（如 5 个）时检测错误函数形式的能力不足，相比之下 TLI/CFI/RMSEA 更敏感；但随着时间点增多 SRMR 表现会改善。传统 SRMR 未包含均值信息，因此 Asparouhov & Muthén (2018) 建议替代计算方式。WRMR 在 WLSMV 下表现不佳，经常错误拒绝模型或无法识别错误模型。

Mplus 自 8.1 版本起，采用了一种能够解决均值信息遗漏问题的 SRMR 版本。对于使用 WLSMV 估计的类别模型，SRMR 也已取代 WRMR 指数。鉴于先前对 SRMR 提出的疑虑，在本章及下一章的示例中，对于连续增长模型，我将同时报告 RMSEA 和 SRMR；而对于类别增长模型，则报告 SRMR。

研究建议不要依赖单一的一般拟合指标，而应使用特定的比较模型的 LR 检验，检查函数形式、方差齐性、遗漏变量等具体来源的缺乏拟合（Leite & Stapleton, 2011；Wu et al., 2009）。

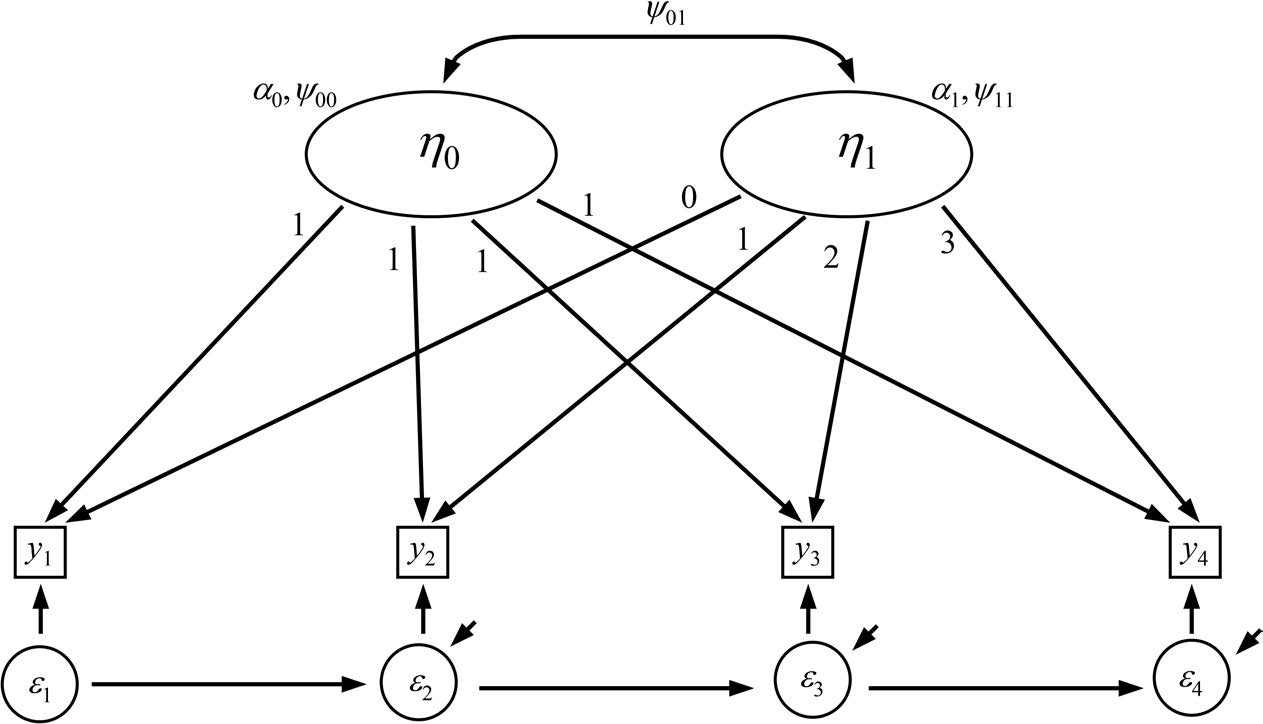
相关残差

在多时间点研究（如 daily diary）中，残差相关可捕捉周期性，或延续效应（carryover effect）。单指标模型默认不含残差相关，但可加入。估计 lag-1 自相关需 ​J-1 个参数，而完全残差相关需 ​J(J-1) 个参数，因此三次测量无法估计任何结构。

残差自相关不影响截距与斜率的均值（因均值由观测均值决定），但会显著影响其方差与协方差，因为残差相关会吸收部分观测协方差。例如：

\mathrm{Cov}(y_1,y_2) = \psi_{00} + \lambda_{11}\lambda_{21}\psi_{11} + (\lambda_{11}+\lambda_{21})\psi_{01} + \mathrm{Cov}(\varepsilon_1,\varepsilon_2). \quad (7.13)

若遗漏真实的 ​\mathrm{Cov}(\varepsilon_1,\varepsilon_2)=\theta_{12}\neq 0，则增长因子的方差与协方差会偏误；特别是 ​\theta_{12}>0 时，截距–斜率协方差会被推向 0 或改变符号。

因此，在时间点足够多且模型可收敛时，允许所有残差相关通常最安全；若受限，则可采用简化结构（如 AR(1) 或相同长度滞后的滞后系数相等，即所有的 lag1 都相等，lag2 都相等）。残差相关主要影响方差结构而非均值结构。

Example 7.1

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.1a
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", _header_=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

library(lavaan)
#Basic linear growth curve model;
model7.1a <- '  i =~ 1*bmi1 + 1*bmi2 + 1*bmi3 + 1*bmi4 + 1*bmi5 + 1*bmi6
        s =~ 0*bmi1 + 1*bmi2 + 2*bmi3 + 3*bmi4 + 4*bmi5 + 5*bmi6

    #variances/covariances
i ~~ i
s ~~ s
i ~~ s

    #intercepts
i ~ 1
s ~ 1 
bmi1 ~ 0
bmi2 ~ 0
bmi3 ~ 0
bmi4 ~ 0
bmi5 ~ 0
bmi6 ~ 0  '

fitmodel7.1a <- growth(model7.1a, _data_=health1)
summary(fitmodel7.1a, _fit.measures_=TRUE, _standardized_=TRUE, _rsquare_=TRUE)

采用健康与老龄化数据集（N = 5,335）估计了一个潜增长曲线模型，以 12 年间（共六个波次，每波间隔两年）体重的变化情况。体重通过身体质量指数（BMI）进行测量，该指数为体重与身高平方的比值（kg/m²）。模型设定所有截距因子载荷为 1，斜率因子载荷分别为 0、1、2、3、4、5。初始模型中未包含相关残差。根据相对拟合指数，模型对数据的拟合良好：χ²(16) = 623.877，CFI = .990，SRMR = .031，RMSEA = .084。截距因子均值为 27.211，与第一波观测均值（27.176）几乎完全一致。尽管该值具有统计显著性，但检验仅表明其大于零，因此其显著性通常无关紧要。均值约为 27 表明，在研究开始时，受访者平均处于超重范畴。斜率因子均值为.150（p < .001），意味着每两年 BMI 分数显著增加约 0.15 分。基于斜率方差（.197）、残差方差均值（1.748）及六个时间点，计算得到 Raudenbush 与 Bryk（2002）斜率信度指数：

RB\ \rho = \frac{.197}{[.197 + (1.748 / 6)]} = .403,

该结果表明斜率的估计具有中等程度的信度。

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.1b
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", header=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

library(lavaan)
#linear growth curve model with correlated residuals;
model7.1b <- '  i =~ 1*bmi1 + 1*bmi2 + 1*bmi3 + 1*bmi4 + 1*bmi5 + 1*bmi6
        s =~ 0*bmi1 + 1*bmi2 + 2*bmi3 + 3*bmi4 + 4*bmi5 + 5*bmi6

i ~~ i
s ~~ s
i ~~ s

i ~ 1
s ~ 1 
bmi1 ~ 0
bmi2 ~ 0
bmi3 ~ 0
bmi4 ~ 0
bmi5 ~ 0
bmi6 ~ 0 

bmi1 ~~ bmi2 #add adjacent correlated residuals.
bmi2 ~~ bmi3
bmi3 ~~ bmi4
bmi4 ~~ bmi5
bmi5 ~~ bmi6 '

fitmodel7.1b <- growth(model7.1b, data=health1)
summary(fitmodel7.1b, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

第二个模型在复制首模型的基础上增加了所有残差间的自相关。该模型未能收敛，因此后续模型仅保留相邻时间点残差的相关性（即滞后 1 阶自相关：ε1 与 ε2、ε2 与 ε3 等）。此模型拟合度显著优于无残差相关模型：χ²(11) = 187.542，CFI = .997，SRMR = .031，RMSEA = .055。平均截距与斜率的估计值基本保持不变（27.214 与.151），但方差与协方差估计值发生显著变化：截距方差 22.783（p < .001）、斜率方差.110（p < .001）、截距与斜率因子间协方差.150（p < .001）。该协方差在首模型中未达显著，而在纳入残差相关后显示基线 BMI 与 BMI 随时间变化呈正相关（ψ* = .095）。截距与斜率因子的正协方差表明初始体重较高者随时间推移体重增幅显著更大。值得注意的是，在加入残差自相关后，增长因子间相关系数的符号发生了改变。

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.1c
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", header=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
                   "bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
                   "cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
                   "cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
                   "cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")
library(lavaan)
#growth curve model with equal residual variances
model7.1c <-  '  i=~ 1*bmi1 + 1*bmi2 + 1*bmi3 + 1*bmi4 + 1*bmi5 + 1*bmi6
         s=~ 0*bmi1 + 1*bmi2 + 2*bmi3 + 3*bmi4 + 4*bmi5 + 5*bmi6
  
i ~~ i
s ~~ s
i ~~ s

i ~ 1
s ~ 1

bmi1 ~ 0
bmi2 ~ 0
bmi3 ~ 0
bmi4 ~ 0
bmi5 ~ 0
bmi6 ~ 0

bmi1 ~~ a*bmi1 #set residuals equal for homogeneity test;
bmi2 ~~ a*bmi2
bmi3 ~~ a*bmi3
bmi4 ~~ a*bmi4
bmi5 ~~ a*bmi5
bmi6 ~~ a*bmi6 '

fitmodel7.1c <- growth(model7.1c, data=health1)
summary(fitmodel7.1c, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

https://www.longitudinalsem.com/lsem2/ex7-1a.inp

https://www.longitudinalsem.com/lsem2/ex7-1b.inp

https://www.longitudinalsem.com/lsem2/ex7-1c.inp

随后在一个模型中检验了方差齐性。通过移除相关残差，使得该模型能够与允许异方差的初始模型进行比较。将残差方差限制为随时间相等的模型其卡方值显著高于第一个模型，其中 χ²(21) = 969.387，CFI = .984，SRMR = .026，RMSEA = .092，尽管根据若干替代拟合指数该模型仍具有可接受的拟合度。与异方差模型相比，卡方差异显著且处于中等幅度，Δχ²(5) = 345.510，p < .001，w = .347，ΔNCI = .151。此比较结果及自相关模型的结果表明，线性模型可能不适用，或存在重要的遗漏变量。关于该变量轨迹的进一步研究将在下一章非线性增长曲线模型中进行。

LGCM 在二分类与有序观测变量中的应用

二分类与有序分类变量可以通过 logit 或 probit 回归构建潜在增长模型。以二分类变量为例，个体增长曲线为：

\ln\left[\frac{P(y_{ti}=1)}{P(y_{ti}=0)}\right]= \eta_{0i} + \lambda_{t1}\eta_{1i}.

在已知数据集中其他案例信息的前提下，针对任意给定时间点，将个体观测值等于 1 的概率设想为递增或递减的趋势。更广义地说，我们可以基于潜在连续变量 ​y^*来考量个体线性化的增长曲线：

y_{ti}^*=\eta_{0i}+\lambda_{t1}\eta_{1i}+\varepsilon_{ti},\qquad y_{ti}=1\ \text{if}\ y_{ti}^*>\text{threshold}.

二分类变量通常将唯一阈值固定为 0；多类别有序变量需约束阈值跨时间保持一致，否则水平变化可能仅反映阈值变化。单指标模型中， ​y^* 分布所需的识别约束（无论是 delta 参数化还是 theta 参数化）也隐含着方差齐性的假设。在 delta 参数化中，所有残差 ​\theta_{tt} = \text{Var}(\varepsilon_t) 均被假定等于 1。即使在 theta 参数化中，由于 ​\theta_{tt} 的方差需要对 ​y^* 分布进行标准化设定，等式约束也会对因子方差的正确解释造成问题（Muthén & Asparouhov, 2002），因此并不适用。。

若模型可识别，也可加入残差自相关。对于使用 WLSMV 估计法估计二元观测变量的增长曲线，存在多种可能的尺度设定选项，这些选项可能影响收敛速度和估计偏差，其中将所有测量阈值设为 0 且所有尺度因子设为 1 似乎具有最佳的整体性能（Newsom & Smith, 2020）。对于使用分类 MLR（参见第 1 章）的二元变量，采用逻辑斯蒂模型时，阈值的对数几率可以由第一个时间点的阈值与截距因子均值之间的差值表示。从概念上讲，在个体案例层面， ​y_{ti}=1的概率是案例层面截距的指数函数。：

P(y_{ti}=1)=\frac{1}{1+\exp[-(\alpha_{0i}+\lambda_{t1}\alpha_{1i})]}.

这些模型可与 IRT 框架结合，用于检验测量性质变化或 DIF。

对于使用概率单位(probit)估计的 WLSMV 估计法，需采用正态累积分布函数（cdf）变换来求得 ​y_{ti} = 1的概率。然而，要扩展逻辑函数或正态 cdf 变换以估计在特定时间 ​y_t = 1的预期比例，或估计 ​y_t = 1的概率随时间推移的平均预期增长，并非易事。这是因为当数据为二元时，对各个体斜率所测比例增长取平均值，并不等于平均斜率的比例增长（Masyn, Petras & Liu, 2014）。只有在获得截距与斜率的因子得分值、推导出每个个案的比例增长后，再对所有个案的比例取平均值，才能得到这些估计值。在绘制二元或有序情况下的个体斜率时，同样需要此方法。

尽管组内相关系数和信度可以按照与连续变量情形类似的方式进行概念化，但由于残差方差的约束，需要对 ​\theta_{(tt)}进行修正：在 delta 参数化中令其等于 1，或令 ​\theta_{tt} = \Delta^{-2} - \psi_{00} - \lambda_{t1}^2 \psi_{11} - 2\lambda_{t1} \psi_{01}，其中 ​\Delta为尺度因子，且假定来自 ​\eta_0的所有载荷均为 1。实际应用中，通常将除第一个之外的所有 ​\theta_{tt}约束为相等最为简便（第一个 ​\theta_{tt}通常设为识别约束），以在 ​\theta_{tt} \neq \theta_{11}时获得 ​\text{Var}(\varepsilon_t) = \theta_{tt}的估计值。

Example 7.2 二分变量和等级变量

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.2a
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", header=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
                   "bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
                   "cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
                   "cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
                   "cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

#anomalous R problem with diab3 variable, resolved by recomputing
health1$diab3 = health1$diab3

library(lavaan)
#growth curve model for binary variables
#this specification matches the WLSMV1 described by Newsom & Smith (2020);
#results are the same as Mplus, but this model does not properly converge, 
#as was aslo the case with Mplus,
model7.2a <-  '  
    i=~ 1*diab1 + 1*diab2 + 1*diab3 + 1*diab4 + 1*diab5 + 1*diab6
    s=~ 0*diab1 + 1*diab2 + 2*diab3 + 3*diab4 + 4*diab5 + 5*diab6
  
    i ~~ i
    s ~~ s
    i ~~ s
  
    i ~ 1
    s ~ 1
  
    #thresholds set to 0
    diab1 | 0*t1
    diab2 | 0*t1
    diab3 | 0*t1
    diab4 | 0*t1
    diab5 | 0*t1
    diab6 | 0*t1
  
    #scaling factors set to 1
   diab1 ~*~ 1*diab1
   diab2 ~*~ 1*diab2
   diab3 ~*~ 1*diab3
   diab4 ~*~ 1*diab4
   diab5 ~*~ 1*diab5
   diab6 ~*~ 1*diab6
   '

fitmodel7.2a <- sem(model7.2a, data = health1, estimator= "WLSMV", parameterization = "delta", 
                    ordered=c("diab1", "diab2", "diab3", "diab4", "diab5", "diab6"))
summary (fitmodel7.2a, fit.measures= TRUE, rsquare= TRUE, standardized= TRUE)

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.2b
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", header=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

#create weight categories to illustrate ordinal variables;
health1$wtcat1 [health1$bmi1 < 18.5] <- 1
health1$wtcat1 [health1$bmi1 >= 18.5 & health1$bmi1 < 25] <- 2
health1$wtcat1 [health1$bmi1 >= 25 & health1$bmi1 < 30] <- 3
health1$wtcat1 [health1$bmi1 >= 30] <- 4

health1$wtcat2 [health1$bmi2 < 18.5] <- 1
health1$wtcat2 [health1$bmi2 >= 18.5 & health1$bmi2 < 25] <- 2
health1$wtcat2 [health1$bmi2 >= 25 & health1$bmi2 < 30] <- 3
health1$wtcat2 [health1$bmi2 >= 30] <- 4

health1$wtcat3 [health1$bmi3 < 18.5] <- 1
health1$wtcat3 [health1$bmi3 >= 18.5 & health1$bmi3 < 25] <- 2
health1$wtcat3 [health1$bmi3 >= 25 & health1$bmi3 < 30] <- 3
health1$wtcat3 [health1$bmi3 >= 30] <- 4

health1$wtcat4 [health1$bmi4 < 18.5] <- 1
health1$wtcat4 [health1$bmi4 >= 18.5 & health1$bmi4 < 25] <- 2
health1$wtcat4 [health1$bmi4 >= 25 & health1$bmi4 < 30] <- 3
health1$wtcat4 [health1$bmi4 >= 30] <- 4

health1$wtcat5 [health1$bmi5 < 18.5] <- 1
health1$wtcat5 [health1$bmi5 >= 18.5 & health1$bmi5 < 25] <- 2
health1$wtcat5 [health1$bmi5 >= 25 & health1$bmi5 < 30] <- 3
health1$wtcat5 [health1$bmi5 >= 30] <- 4

health1$wtcat6 [health1$bmi6 < 18.5] <- 1
health1$wtcat6 [health1$bmi6 >= 18.5 & health1$bmi6 < 25] <- 2
health1$wtcat6 [health1$bmi6 >= 25 & health1$bmi6 < 30] <- 3
health1$wtcat6 [health1$bmi6 >= 30] <- 4

library(lavaan)
#growth curve model wtih ordinal indicators;
#Note: slight differences from Mplus output fit and parameter estimates, 
#likely related to differences in WLSMV theta parameterization algorithms
#or handling sparse data, [to see warnings, use warnings(lavaan)]
model7.2b <- '  i =~ 1*wtcat1 + 1*wtcat2 + 1*wtcat3 + 1*wtcat4 + 1*wtcat5 + 1*wtcat6
        s =~ 0*wtcat1 + 1*wtcat2 + 2*wtcat3 + 3*wtcat4 + 4*wtcat5 + 5*wtcat6

i ~~ i
s ~~ s

i ~~ s

i ~ 1
s ~ 1

wtcat1 | 0*t1
wtcat1 | a*t2
wtcat1 | b*t3

wtcat2 | 0*t1
wtcat2 | a*t2
wtcat2 | b*t3

wtcat3 | 0*t1
wtcat3 | a*t2
wtcat3 | b*t3

wtcat4 | 0*t1
wtcat4 | a*t2
wtcat4 | b*t3

wtcat5 | 0*t1
wtcat5 | a*t2
wtcat5 | b*t3

wtcat6 | 0*t1
wtcat6 | a*t2
wtcat6 | b*t3  

'

fitmodel7.2b <- growth(model7.2b, data=health1, parameterization="theta", estimator="wlsmv", 
        ordered=c("wtcat1", "wtcat2", "wtcat3", "wtcat4", "wtcat5", "wtcat6"))
summary(fitmodel7.2b, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

https://www.longitudinalsem.com/lsem2/ex7-2a.inp

https://www.longitudinalsem.com/lsem2/ex7-2b.inp

二分变量

使用六次每二年测一次的数据，采用 WLSMV 与 delta 参数化，并将所有测量阈值设为 0、​y^* 残差方差固定为 1。模型拟合良好（加权 ​\chi^2(16)=363.600, CFI=.993, SRMR=.037）。截距均值估计为 -1.346，其正态累积概率为：​\Phi(-1.346)=0.091,

与样本中基线糖尿病比例（9.1%）一致。斜率均值为 0.081（​p<.001），表示每两年患病比例增加。截距与斜率方差显著（分别为 ​1.011 与 0.024），说明个体间在基线患病率与变化率上存在差异。斜率信度为：​\rho_1=\frac{\psi_{11}}{\psi_{11} + 1/6} =\frac{.024}{.024 + 1/6} = .219,

显示斜率信度较低。

有序分类例子（四分类 BMI）

将 BMI 按国际标准分为四类，设置第一个阈值为 0，其余阈值跨时间保持相等以确保度量一致。模型采用 WLSMV 与 theta 参数化，拟合良好（​\chi^2(26)=203.148, CFI=1.000, SRMR=.008）。截距均值为 7.155、斜率均值为 0.107（均 ​p<.001），代表 ​y^* 在标准正态量表上每两年增加 0.107。标准化斜率为 .284，为中等大小，略低于连续 BMI 的斜率结果。截距方差 ​16.550 与斜率方差 ​0.143 均显著，表示个体在初始水平与变化速度上存在差异。

delta 或 theta 参数化在理论上是等价的，其解可相互转换（Kamata & Bauer, 2008；Muthén & Asparouhov, 2002）。因此，选择 delta 或 theta 参数化主要取决于研究者希望在模型中如何表达与约束测量残差方差以及潜在连续响应变量的尺度，而非统计上的优劣。

Newsom & Smith(2020)的研究中提到提到二分变量潜在增长模型在不同估计方法下（WLSMV 的三种参数化与 MLR）的表现，结果显示：WLSMV1、WLSMV2 与 MLR 在样本量足够大（约 N≥500）且时间点较多（T≥5）时能提供偏差较小、标准误与覆盖率较为准确的估计；而 约束最少的 WLSMV3 因无法有效识别二分变量潜在响应分布方差，表现最不稳定，常出现方差估计偏差大、标准误不准确、不当解与覆盖率不足等问题，因此不推荐使用。MLR 的整体表现与 WLSMV1/2 相近，在部分条件下略优。研究指出，二分指标对量尺约束极为敏感，适当的方差与阈值约束反而是保证识别与稳定估计的关键。此外，作者指出当指标为有序多类别变量时，阈值信息更丰富、识别相对容易，因此估计质量通常优于二分情况，但 WLSMV/MLR 仍是最稳健的选择。总体而言，二分或有序 LGCM 推荐使用带适当量尺约束的 WLSMV 或 MLR，并尽可能增加样本量与测量波次，以确保均值、斜率方差等关键参数的可靠估计。

时不变协变量与跨层交互作用

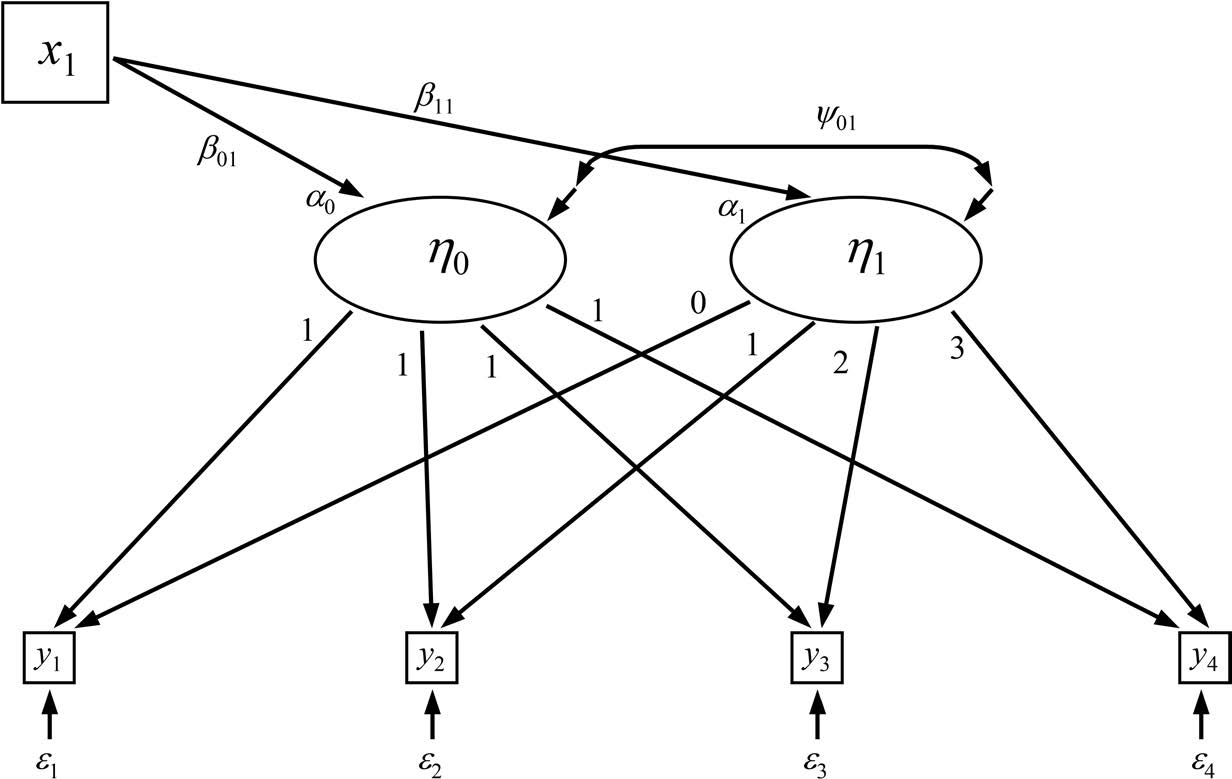
本节讨论在增长曲线模型中加入一次测量的时间不变协变量（TIC） ，以解释个体间在截距与斜率上的差异。 加入 TIC (​x_{1i}) 后，无条件增长模型变为

\eta_{0i} = \alpha_0 + \beta_{01} x_{1i} + \zeta_{0i},
\eta_{1i} = \alpha_1 + \beta_{11} x_{1i} + \zeta_{1i}.

将上式代入测量方程

y_{ti} = \eta_{0i} + \lambda_{t1}\eta_{1i} + \varepsilon_{ti},

得到单层形式的模型：

y_{ti}= \alpha_0 + \alpha_1 \lambda_{t1} + \beta_{01} x_{1i} + \beta_{11} \lambda_{t1} x_{1i} + \zeta_{0i} + \zeta_{1i}\lambda_{t1} + \varepsilon_{ti}.

其中项 ​(\lambda_{t1} x_{1i}) 即为时间得分与协变量的乘积，​(\beta_{11}) 为该跨层交互项的回归系数。

若 ​\beta_{11} 显著，则意味着不同水平的 x 会改变个体随时间的变化速度。例如，在 BMI 的增长模型中，若年龄预测斜率，则老年人与年轻人的 BMI 随时间变化的速率不同，可表现为更快上升、更快下降，或不同方向的混合趋势。

加入 TIC 是无条件模型之后常见且直接的扩展，但需考虑模型设定、理论依据及交互的解释性。

自变量的量尺约束

在增长曲线中加入交互项时，自变量的量尺（scaling）很关键：

  1. 和一般回归一样，加入乘积项后会产生较强多重共线性，不会影响交互项系数本身及其显著性，但会增大主效应的标准误。可以通过对预测变量做中心化来缓解：

    • 观测变量：用偏差分数 ​(x_i - \bar x)；
    • 潜变量：可对指标做中心化，或直接将因子均值约束为 0，或用改进的效应编码法令 ​(\mu_\eta = 0)。

  2. 在潜在增长模型中，量尺还严重影响截距的含义。线性变换通常不影响斜率，但会改变截距解释：例如，以“年龄”预测 BMI 增长，若年龄不中心化，则截距表示“年龄为 0 岁时、研究起点的预期 BMI”，往往没有实际含义。

  3. 一旦模型中有多个预测变量，截距表示“所有预测变量都等于 0 时的预期 (y)” 。若这些 0 点都不合理（比如收入=0、年龄=0、主观幸福感=0），截距的解释也不合理。

因此，一般应将 TIC 进行中心化或重新标定，使 0 点有清晰、可解释的含义，然后再解释增长曲线的截距。

跨层级交互作用

在增长模型中，如果 TIC 预测斜率且交互显著，研究者通常通过作图和简单斜率来解释交互效果。简单斜率描述了在协变量特定取值下，时间与结果变量之间的关系，即协变量水平不同的人随时间变化的速率不同。常用的协变量取值为 −1 SD、0、+1 SD；若协变量是潜变量，则用其方差平方根作为 SD。

Curran、Bauer 与 Willoughby（2004）将预测变量​x_1对斜率因子​\eta_1的简单斜率称为简单轨迹。该简单轨迹可描述为在协变量取特定值（例如​-sd_x、0 或​sd_x）时，调整协变量效应后的潜斜率变量条件均值。

简单斜率（简单轨迹）的条件平均值为

\alpha_{1|x_1}= \alpha_1 - \beta_{11} x_1,

其中 ​(\alpha_1) 是斜率的总体均值（协变量已中心化），​(\beta_{11}) 是斜率回归到协变量的系数，​(x_1) 是选定的协变量值。

简单截距用于绘图，其公式为

\alpha_{0|x_1}= \alpha_0 - \beta_{01} x_1.

对每个时间点 ​(t)，预测值由

\hat y_{t|x_1}= \alpha_{0|x_1} + \alpha_{1|x_1}\lambda_{t1}

得到，其中 ​(\lambda_{t1}) 为时间得分。选择不同的 ​(x_1)（如 −1 SD、0、+1 SD）即可绘制不同的增长曲线。

简单斜率可通过 Wald 比率检验其显著性：

\frac{\alpha_{1|x_1}}{SE(\alpha_{1|x_1})}.

其标准误为

SE_{\alpha_{1|x_1}}=\sqrt{\widehat{\operatorname{Var}(\alpha_1)}+2x_1 \widehat{\operatorname{Cov}(\alpha_1,\beta_{11})}+x_1^{2}\widehat{\operatorname{Var}(\beta_{11})}}

若 Wald 比率大于 1.96（​\alpha=.05），则简单斜率显著。计算这些值需使用模型的渐近方差–协方差矩阵。

除了简单斜率，还可使用 Johnson–Neyman 区域、条件截距或斜率的置信带，或比较某时间点的预测值，以进一步探讨交互效应的性质。

轨迹的组间差异

MIMIC

当 TIC 是二分类或多分类变量时，增长曲线模型可视为 MIMIC（multiple-indicator multiple-cause）模型的推广。此时协变量由 ​(G-1) 个虚拟变量表示，其对斜率因子 ​(\eta_1) 的回归即对应组别 × 时间的交互效应，与混合设计 ANOVA 中的组别 × 重复测量交互完全类似。

在该情境中，协变量对斜率因子的路径系数 ​(\beta_{11}) 表示两组斜率的差异：

\beta_{11} = \alpha_{1g1} - \alpha_{1g0},

其中 ​(\alpha_{1g0}) 与 ​(\alpha_{1g1}) 分别表示组 0 与组 1 的平均斜率，也就是 Equation (7.14) 中的两个简单轨迹。

模型中的斜率截距（路径标记为 ​\alpha_1）是组 0 的条件平均斜率：

\alpha_{1g0} = \alpha_1,

对其显著性检验即是组 0 的简单轨迹是否不同于 0（与 Equation (7.15) 相同）。组 1 的简单轨迹可通过交换组别编码（例如从 0/1 改为 1/0）得到其显著性检验。

需要注意的是，分组变量的编码会影响简单轨迹的解释。若将组别编码为 1 与 2，则“0 组”不存在，​\alpha_1的含义不再合理。此外，常见做法是将二分类变量中心化，使 ​\alpha_1表示两组平均斜率，这在许多研究中是有意义的。

多组

多组增长曲线模型是另一种检验组间差异的方法。做法是为每个组分别建立基本增长模型（如 Figure 7.3），并通过嵌套模型比较对关键参数（均值、方差等）施加或解除约束，从而检验组间是否相同。

多组方法的优势在于可比较各组的截距方差与斜率方差，回答“基线的变异量是否不同”“变化速率的变异量是否不同”等问题，而这些是 MIMIC 模型无法检验的。各组模型内部也可加入 TIC，从而检验三重交互；例如，若性别为分组变量，而 ​(x_1) 是二分类预测变量，则比较两组的 ​(\beta_{11}) 等价于检验一个 ​(2\times 2 \times T) 的交互，其中 ​(T) 代表线性趋势。比如，可检验“母语（英语/西班牙语）× 性别（女/男）× 经济安全感随时间变化”是否存在交互。

多组方法还能灵活处理误差结构，允许组间残差不同，以建模方差异质性；而 MIMIC 必须假设误差方差跨组一致。此外，多组框架还能比较不同组的轨迹是否具有相同的函数形式（如线性、非线性）。

探索性方法

根据个体的变化模式对其进行分类，再考察各类群体的特征。例如，可将个体按其经济安全感随时间的变化划分为：持续上升、持续下降、持续偏低、持续偏高等类型。分类完成后，可进一步分析各组的社会人口学特征或其他相关变量。

这种方法比直接预测斜率增加或减少更能捕捉细微且具质性意义的变化模式。常见做法是先保存截距与斜率的因子分数，再利用这些分数进行图形探索、聚类分析（Dumenci & Windle, 2001）、判别分析等，从而形成轨迹类型或识别影响轨迹类型的特征。

Example 7.3：含时不变协变量的增长曲线

https://www.longitudinalsem.com/lsem2/ex7-3a.inp

https://www.longitudinalsem.com/lsem2/ex7-3b.inp

https://www.longitudinalsem.com/lsem2/ex7-3c.inp

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.3a
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", _header_=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

#center age
health1$age <- health1$age - mean(health1$age)

library(lavaan)
#growth curve model with age as time invariant covariate;
model7.3a <- '  i =~ 1*bmi1 + 1*bmi2 + 1*bmi3 + 1*bmi4 + 1*bmi5 + 1*bmi6
        s =~ 0*bmi1 + 1*bmi2 + 2*bmi3 + 3*bmi4 + 4*bmi5 + 5*bmi6
  
  

    #variances/covariances
i ~~ i
s ~~ s
i ~~ s

    #intercepts
i ~ 1
s ~ 1 
bmi1 ~ 0
bmi2 ~ 0
bmi3 ~ 0
bmi4 ~ 0
bmi5 ~ 0
bmi6 ~ 0  

#predicing intercept and slope
i + s ~ age

#remove comment to add correlated residuals as in ex7.1b
#bmi1 ~~ bmi2 
#bmi2 ~~ bmi3
#bmi3 ~~ bmi4
#bmi4 ~~ bmi5
#bmi5 ~~ bmi6 
'

fitmodel7.3a <- growth(model7.3a, _data_=health1)
summary(fitmodel7.3a, _fit.measures_=TRUE, _standardized_=TRUE, _rsquare_=TRUE)

以参与者基线年龄作为 TIC，对 BMI 的条件增长曲线模型进行了检验。该模型基于示例 7.1 中的无条件模型。年龄通过从每个个体的得分中减去样本均值（55.975）进行中心化。尽管模型的卡方检验显著，​\chi^2(20)=641.026,, p<.001，但其他拟合指数表明模型拟合度较好，CFI = .989，SRMR = .028，RMSEA = .076。年龄与基线 BMI 并无显著关系， ​\beta_{01} = - .011，ns，但年龄与斜率因子显著相关， ​\beta_{11} = - .015,p<.001，表明存在跨层交互作用。标准化系数显示该交互作用对斜率的影响相对较小， ​\beta_{11}^* = - .141。截距因子的条件均值为 27.211，表示平均年龄人群的初始 BMI 分数。斜率因子的条件均值表明，对于平均年龄者，每一波次 BMI 分数约增加 0.15， ​\alpha_1 = .150, \alpha_1^* = .337, p<.001。由于无条件模型显示 BMI 整体上升，跨层交互作用的负系数表明，基线年龄越大，BMI 随时间的增长越缓慢。

年龄的标准差为 4.095，并使用该值在协变量上推导用于绘图和简单轨迹检验的三个点。将数值 −4.095、0 和 4.095 代入先前得到的条件均值和协变量路径估计，得到三个简单轨迹值：

\alpha_1 - x_i \beta_{11} = \alpha_{1|x_i}
.150 - (-4.095)(-.015) = .211
.150 - (0)(-.015) = .150
.150 - (4.095)(-.015) = .089

这些简单轨迹表明：当年龄比平均值低一个标准差时，每一波次 BMI 增加 .211 点。对于平均年龄者，增加值为 .150，与样本整体平均值相同。对于年龄比平均值高一个标准差者，每一波次的 BMI 增加量较小，为 .089 点。从输出中获得了参数方差与协方差估计，并使用公式 (7.16) 计算了每个简单轨迹的 Wald 比率，结果表明每个值均显著大于 0。对于低、平均和高年龄值，其比率分别为：​.211/.010 = 20.000,, p<.001, ​.15/.007 = 20.05,, p<.001, 以及 ​.089/.010 = 8.373,, p<.001。虽然简单轨迹均显著，但显著的跨层交互作用意味着它们的效应大小并不相同。

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.3b
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", header=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

#create binary version of age for illustration purposes
#can reverse codes for other simple trajectory;
health1$agecat [health1$age >= 65] <- 1
health1$agecat [health1$age < 65] <- 0

library(lavaan)
#growth curve model with age groups as binary time invariant predictor;
model7.3b <-  ' i =~ 1*bmi1 + 1*bmi2 + 1*bmi3 + 1*bmi4 + 1*bmi5 + 1*bmi6
        s =~ 0*bmi1 + 1*bmi2 + 2*bmi3 + 3*bmi4 + 4*bmi5 + 5*bmi6

i ~~ i
s ~~ s
i ~~ s
i ~ 1
s ~ 1

bmi1 ~ 0
bmi2 ~ 0
bmi3 ~ 0
bmi4 ~ 0
bmi5 ~ 0
bmi6 ~ 0

i + s ~ agecat  ' 

fitmodel7.3b <- growth(model7.3b, data=health1)
summary(fitmodel7.3b, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

为了说明带有二元协变量的潜在增长曲线模型，研究者在此将年龄在 65 岁处进行人工二分（50–64 岁 vs. ≥65 岁）。我并不推荐这种做法，但在此情境下，人工二分对于教学目的具有一定的示范作用。首先采用 MIMIC 方法，将截距因子和斜率因子回归于该二元年龄变量，此方法与刚才介绍的以连续年龄为协变量的模型完全相同。二元年龄变量对截距因子的预测并不显著， ​\beta_{01} = - .568，ns，表明在基线时 BMI 不存在显著的年龄差异。这一不显著差异意味着，在基线时，65 岁以上组的平均 BMI 略低。另一方面，年龄类别对斜率因子是显著预测变量，提示存在跨层交互作用， ​\beta_{11} = - .157, p<.05。斜率的条件均值（协变量—斜率因子回归中的截距）是显著的，​\alpha_1 = .152, p<.001。由于年龄类别被编码为 0 和 1，该条件均值同时也代表 65 岁以下者（即 0 组）的简单轨迹，​\alpha_{1|\text{<65}}。为了获得另一条简单轨迹的取值，我将年龄类别变量重新编码，使 0 表示 ≥65 岁、1 表示 <65 岁。该模型得到的条件均值为 ​\alpha_{1|\le 65} = - .005，且并不显著。结果表明，对于研究开始时年龄在 65 岁以下的个体，BMI 呈线性上升；而对于 65 岁及以上的个体，BMI 并未显著增加。需要指出的是，对于连续变量也可以使用类似的计算机方法，通过将均值中心化到特定取值（例如 −1 个标准差、原始均值和 +1 个标准差）来进行。

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.3c
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", header=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

#create binary age for groups
health1$agecat [health1$age >= 65] <- 1
health1$agecat [health1$age < 65 ] <- 0

library(lavaan)
#multigroup growth curve model comparing age groups;
#second test of this model constrained the slopes to be equal;  
model7.3c <-  ' i =~ 1*bmi1 + 1*bmi2 + 1*bmi3 + 1*bmi4 + 1*bmi5 + 1*bmi6
        s =~ 0*bmi1 + 1*bmi2 + 2*bmi3 + 3*bmi4 + 4*bmi5 + 5*bmi6

i ~~ i 
s ~~ s
i ~~ s
i ~ 1
s ~ 1 
#change above to s ~ a*1 to test for group difference (adding equality constraint);

bmi1 ~ 0
bmi2 ~ 0
bmi3 ~ 0
bmi4 ~ 0
bmi5 ~ 0
bmi6 ~ 0 
'

fitmodel7.3c <- growth(model7.3c, data=health1, group="agecat", group.equal="lv.variances") 
summary(fitmodel7.3c, fit.measures=TRUE, standardized=TRUE, rsquare=TRUE)

采用多组方法也检验了同一关于年龄差异的轨迹假设，将 65 岁以下者与 65 岁及以上者进行比较。当允许两组的斜率因子均值分别估计时，模型拟合为 ​\chi^2(34) = 633.351,, p<.001,, \text{CFI} = .990,, \text{SRMR} = .047,, \text{RMSEA} = .081. 当将两组斜率因子的条件均值约束为相等时，​\chi^2(35) = 639.474,, p<.001，卡方值显著增加，​\Delta\chi^2(1) = 6.124,, p<.001。这一差异表明，65 岁以下组的 BMI 斜率为 .152，​p<.001，而 65 岁及以上组的 BMI 斜率为 −.009，ns，两者彼此之间存在显著差异。这些系数估计与采用 MIMIC 模型方法所得的条件均值非常接近。以类似方式，还可以比较各组之间的截距因子均值、截距因子方差、斜率因子方差以及截距—斜率协方差。

时变协变量

在潜在增长曲线模型中，另一种加入额外变量的方法是使用时间变化协变量（time-varying covariates, TVCs） ，即在每个时间点都测量的协变量。TIC 的主要作用是解释截距或斜率之间的个体差异，而 TVC 的作用在于解释各时间点因变量的特定误差，减少每个波次的残差，从而提高斜率因子的估计精度。

加入 TVC 后，层级 1（时间水平）的模型变为：

y_{ti}= \alpha_0 + \lambda_{t1}\alpha_1 + \lambda_{t1}\zeta_{1i} + \zeta_{0i} + \beta_{tt}\,x_{ti} + \varepsilon_{ti},

其中 ​(x_{ti}) 是在时间点 ​(t) 测得的协变量，系数 ​(\beta_{tt}) 带双下标表示每个时间点的效应可能不同。在多水平传统框架中，通常默认该效应恒定，除非特别加入“时间 × 协变量”交互（McNeish & Matta, 2018）。

若将原本的增长方程（截距与斜率因子）

\eta_{0i} = \alpha_0 + \zeta_{0i},\qquad \eta_{1i} = \alpha_1 + \zeta_{1i}

代入，可写为单一方程：

y_{ti}= \alpha_0 + \lambda_{t1}\alpha_1 + \beta_{tti}x_{ti} + \lambda_{t1}\zeta_{1i} + \zeta_{0i} + \varepsilon_{ti}.

该式清楚展示：每个时间点的因变量 ​(y_{ti}) 同时由 TVC、截距因子、斜率因子及误差决定。若 TVC 的效应 ​(\beta_{tt}>0)，其解释掉部分时点特定误差，会影响无条件模型中其他参数（如斜率方差、截距–斜率协方差等）的估计值。

此外，因为 TVC、截距因子、斜率因子都是外生变量，模型中默认应估计它们之间的协方差（如 Figure 7.7 所示），以确保模型适当识别并呈现真实结构。

自变量的量尺约束

包含 TVCs 时，增长模型中的平均斜率与截距都变成“调整后的均值”，因此解释会受到协变量量尺的强烈影响。与 TIC 类似，若协变量的 0 点在实际中无意义（如 Likert 量表的最低分为 1），则用原始量尺解释 adjusted 均值会导致不合理的推论。因此必须考虑对 TVC 进行适当的重新标定或中心化。

将 TVC 简单中心化为

x_{ti}^* = x_{ti} - \bar{x}_t

（在每个时间点减去当时的均值）会使所有时间点的 TVC 均值为 0，但这种方式会消除 TVC 随时间的趋势信息，使模型只解释“相对于当时平均水平的偏差”，而忽略了协变量本身的整体上升或下降趋势。对于希望控制应激与婚姻冲突随时间共同上升的例子，这种中心化方式会令冲突的调整均值仍然随时间上升，与“没有控制 TVC 时”的现象几乎相同。

另一方式是以基线为参照中⼼化：

x_{ti}^* = x_{ti} - x_{1i},

即“基线中心化”。这样模型解释的是“在基线水平下”的调整均值，并保留个体协变量随时间的相对变化。若应激随时间上升，则冲突在后期会被调整为更接近基线时期的较低水平。

传统的“总体均值中心化”（grand-mean centering）将 TVC 每次测量都减去总体均值，但该总体均值是所有时间点与所有个体的平均值，这在纵向情境下通常不是理想的参考点。

还可以采用“个体平均中心化”：

x_{ti}^* = x_{ti} - \bar{x}_i,

即 within-person centering，强调个体相对自己的偏差，这会改变截距含义，使其不再相对于基线。改良方式为“within-person baseline centering”：

x_{ti}^* = x_{ti} - \bar{x}_i + x_{1i},

即保持相对个体平均的偏差，同时保留基线参照点，使解释回到第一个时间点。

不同中心化方式会改变协方差结构并影响调整均值的解释。理论上都不是错的，但若使用不当，解释会错误，因此必须谨慎选择（详见 lgina & Swaminathan [2011], Enders & Tofighi [2007], and Hoffman [2015, Chapter 9] for indepth discussions of centering）。

包含 TVC 的模型控制的是“时点特定（occasion-specific）”的协变量影响，而不是协变量的整体趋势。它更像是在控制协变量的短期波动，而非建模其长期变化。若想建模 TVC 的整体趋势，应使用“平行增长模型”（parallel process model），即为协变量建立自己的截距与斜率因子，再用它们预测结果变量的增长因子。

许多作者指出，如不区分 TVC 的 within-person 与 between-person 成分，系数可能偏误。完全分离两者需：

  1. 对 TVC 做个体内中心化

    _{ti}^* = x_{ti} - \bar{x}_i,

  2. 将个体平均​\bar{x}_i当作 TIC 加入模型。

此时：

  • 个体平均（TIC）代表 between-person 效应；
  • 个体偏差（TVC）代表 within-person 效应。

这样才能同时估计个体之间差异与个体自身随时间波动的影响。

中心化方法
公式
如何操作（对数据做什么）
保留/丢失的信息结构
对增长模型（LGM）参数的影响
解释方式（Intercept & Slope）
优点与可能问题
1. 不中心化（Raw scores）
$$x^*_{ti} = x_{ti}$$

不做任何处理

完全保留：平均变化 + 个体变化 + 波次特定波动

斜率与截距是 关于 covariate = 0 时的调整均值；但 0 可能没有意义
截距解释为：当协变量 = 0 时的平均初始水平；斜率解释为：控制协变量后随时间的平均变化
解释困难（如 Likert=1 时 0 不存在）；容易得到非自然参照点
2. 波次内中心化（Centering within time point）

$$x^*_{ti} = x_{ti} - \bar{x}_t$$

每个案例的得分减去该波次的总体均值

移除时间趋势；仅保留波次特定偏差（occasion-specific deviation）
斜率基于“该波次平均协变量水平”调整后的均值；不能控制协变量随时间增长
截距/斜率解释为：协变量处于该波次平均水平时的结果平均值
会掩盖协变量真实随时间的变化；结果看起来像“没控制协变量”
3. 基线均值中心化（Baseline mean centering）
$$x^*_{ti} = x_{ti} - \bar{x}_1$$

用样本的 T1 均值作为参照点

保留时间趋势；保留个体差异；丢失整体水平差但保留相对变化
斜率 = 控制协变量随时间变化后的增长
截距解释为：协变量处在“样本基线平均水平”时的结果均值；斜率解释为：在基线水平调整后随时间的变化
更有意义的参照点；但参照点固定在样本基线，可能缺乏理论意义
4. 个体内均值中心化（Within-person / group-mean centering）
$$x^*_{ti} = x_{ti} - \bar{x}_i$$
每个人的得分减去该个人的平均值
分离 within-person 与 between-person 成分（需同时加入 $\bar{x}_i$
产生两个回归效应：
• TVC → 纯 within-person effect
• TIC$\bar{x}_i$→ between-person effect

斜率 = 当个体偏离其自身平均协变量水平时的变化；截距意义改变（不再是 T1）
可完全分离组内与组间效应；但改变了协方差结构，结果与常规模型差异大
5. 基线个体中心化（Within-person baseline centering）
$$x^*_{ti} = x_{ti} - \bar{x}_i + x_{1i} $$
同时使用个体基线作为参照点
保留个体趋势；保持对 T1 的参照意义
类似于方法4，但增加了 T1 参照点，使截距更容易解释
截距解释为：当协变量处于个体自身 T1 水平时的结果水准
最自然的解释；但计算更复杂、转化程度大

同步路径的解释

TVC 的同步路径（synchronous path）系数 ​\beta_{tt} 表示的是协变量与因变量在同一时间点的关联，而不是协变量对因变量“变化”的预测。因此，它反映的是跨波次的共时关系，而非增长或趋势的影响。

在理论上或因识别问题，可将所有 ​\beta_{tt} 设置为相等（同一效应），并通过嵌套模型比较来检验该约束是否合理。然而，协变量与因变量的关系未必随时间保持恒定，因此这种约束必须谨慎使用。

一些研究者提出使用滞后效应（lagged effect） ，即将因变量 ​y_t 回归到前一时间点的协变量 ​x_{t−1}（除了 ​t=1）。滞后模型可以包含同步效应，也可以省略同步效应：

  • 同时包含同步与滞后路径可能导致估计困难，通常需要对路径施加一些等值约束；
  • 省略同步路径则隐含假设协变量只对因变量产生“延迟效应”，没有即时影响；但在经验数据中，同步关系往往比滞后关系更强，因此该假设不一定合理。

无论同步还是滞后路径，模型都没有考虑因变量本身的自回归结构（autoregression） ，即未建模 ​y_t 对 ​y_{t−1} 的影响（尽管部分文献探讨了加入 autoregressive 结构的方法，如 Curran et al., 2014）。

Example 7.4: Time-Varying Covariate

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.4
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", _header_=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

#grand mean centering srh1 and center subsequent waves around this value
health1$srh = health1$srh1 - mean(health1$srh1)

library(psych)
health1$srh2 = health1$srh2 - health1$srh
health1$srh3 = health1$srh3 - health1$srh
health1$srh4 = health1$srh4 - health1$srh
health1$srh5 = health1$srh5 - health1$srh
health1$srh6 = health1$srh6 - health1$srh

library(lavaan)
#growth curve model of BMI with SRH as time varying covariate;

#Note: differences from Mplus in the fit values, but
#other results are very close or identical  
#subequent model constrained covariate effect to be equal by adding (1);
model7.4 <- '  
  i =~ 1*bmi1 + 1*bmi2 + 1*bmi3 + 1*bmi4 + 1*bmi5 + 1*bmi6
  s =~ 0*bmi1 + 1*bmi2 + 2*bmi3 + 3*bmi4 + 4*bmi5 + 5*bmi6

  i ~~ i
  s ~~ s
  i ~~ s
  
  i ~ 1
  s ~ 1 
  bmi1 ~ 0
  bmi2 ~ 0
  bmi3 ~ 0
  bmi4 ~ 0
  bmi5 ~ 0
  bmi6 ~ 0 
  
  bmi1 ~ srh  
  bmi2 ~ srh2
  bmi3 ~ srh3
  bmi4 ~ srh4
  bmi5 ~ srh5
  bmi6 ~ srh6  
  #subsequent model added equality constraints for initial model 
  #change above statements to bmi1 ~ a*srh, bmi1 ~ a*srh2 etc.using constant a for each wave
'

fitmodel7.4 <- growth(model7.4, _data_=health1, _information_ = "observed")
summary(fitmodel7.4, _fit.measures_=TRUE, _standardized_=TRUE, _rsquare_=TRUE)

https://www.longitudinalsem.com/lsem2/ex7-4.inp

这个例子考察 BMI 的增长轨迹，同时控制每个时间点的自评健康作为 TVC。自评健康在每个时间点都以基线平均值中心化，计算方式为

\text{srh}^*_{ti} = \text{srh}_{ti} - \text{srh}_{1}.

初始模型中，每个时间点的健康 →BMI 路径都自由估计。模型拟合不理想（​\chi^2(46)=1085.064, CFI=.983, SRMR=.069, RMSEA=.065），可能是残差相关、遗漏变量或轨迹形式不正确造成的。

自评健康对 BMI 的影响只在第一波显著（−.111, p<.001），标准化系数介于 .002 到 −.025，效应极小。截距均值为 27.209，与无条件模型几乎一致；斜率均值 .151 也与无条件模型相近。截距与斜率方差（23.232 和 .197）同样与无条件模型几乎一致。

接着，将所有健康 →BMI 的路径设为相等并做比较。施加等值约束后的模型拟合稍差（​\chi^2(51)=1095.066），但差异仅在边界显著水平（​\Delta\chi^2(5)=10.002, p=.075），表示健康对 BMI 的影响随时间的变化并不大。

对时间的再思考

最常见的潜在增长曲线模型假设资料来自规则的面板设计，也就是

  1. 数据完整
  2. 每个个体的测量间隔相同
  3. 所有人都在相同的时间点开始与结束测量

这些条件一起构成“时间结构化”（time structured）。

数据缺失

纵向研究中几乎一定会出现缺失资料，因此并非所有受试者在每个时间点都有数据。大致可以区分两种缺失模式：

  1. 间歇性缺失（intermittent missing） ：某些时间点缺测，但后续波次仍有资料。
  2. 流失（attrition） ：某个个体在研究末期的一个或多个连续时间点完全缺测。

这两种模式的界线并不总是清楚，例如最后一个时间点缺测的个案，无法轻易判断其是否属于流失。一般认为间歇性缺失更可能符合“随机缺失”（MAR），但这并非必然。若数据至少可假定满足 MAR 条件，则全信息最大似然估计在多数结构方程模型软件中易于实施，并能提供优质的参数估计。若数据不满足 MAR 条件，则需考虑其他处理方法。关于纵向模型中缺失数据问题的更详尽探讨可参见第 14 章。

非等距测量

直接使用假设的时间点而非真实测量时间，可能造成：

  • 截距与斜率方差的正偏，
  • 截距–斜率协方差的负偏，

尤其当真实测量时间分布偏斜时更明显。增加测量次数与样本量可以减轻这种偏差。

在分析数据前, 检查任何给定数据集中的实际测量时间是否至少大致符合假定的时间结构。有些做法（如将日期取整到特定日期）在某些情况下可能产生重要偏差。例如，在婴儿研究中按月龄取整可能导致结果基于一个比“整数月龄”更大的实际发展年龄；尽管此问题对较高年龄影响甚微，但在数周甚至数天的发展差异都很重要的婴幼儿研究中，其影响可能十分显著。

只要数据是时间结构化的，并且存在真实的不等间距观测，估计潜在增长曲线通常并无特别问题。因子载荷可被调整以恰当地反映间距差异。例如，一项调查前三个波次按年度进行，而后续三波按两年一次进行，那么可将时间编码设为 0、1、2、4、6 和 8。这样，斜率因子的均值便表示每一“年”在 yt 上的变化量，而年增长率在后面三个两年一次的波次中是基于较短区间估计的。

在其他情形中，数据可能远不如上述情况有序，且不同个体的测量间隔长度可能不同。取决于个体间变异的程度，缺失数据估计方法与适当的斜率载荷编码的组合可能足以应对问题。如果不同个体在测量间隔的规则性上存在相当大的差异，则可使用对这些个体真实时间点的特殊估计方法。

最典型的例子是队列序列设计（cohort sequential / accelerated design） 。该设计包含多个不同的队列，但每个队列都被追踪相同的时间长度。例如，研究者同时追踪 18、19、20、21 岁进入大学的学生，每个队列都被连续追踪四年。

由于各队列在 Time 1 的年龄不同，若把年龄作为时间量尺，每个学生的“起点年龄”与“终点年龄”自然不同，这就造成了不同个体的起止时间差异。

面对多队列或不同起始年龄的情况，有几种处理方式。

  1. 把队列（例如起始年龄）当作 TIC 处理。比如将年龄作为协变量加入模型。忽略年龄差异，让所有人共享同一个截距与斜率。
    在大学生的例子中，研究者不关心大一学生进入大学时年龄不同，而选择估计跨年龄组的共同截距与斜率。只要研究目的在于为所有年龄推导单一的估计值，这种控制年龄的方法就不会产生问题。
    在此情境及其他情境中，重要的是谨慎考虑协变量的编码方式，特别是应注意通常需要某种形式的中心化操作。若以平均年龄中心化，则截距被解释为第一波（若斜率因子的载荷为 ​t = 0,1,2,\ldots）时因变量的估计值；若未中心化，则截距将被解释为出生时因变量的预期值。若围绕最早可能年龄进行中心化（即从理论上选择一个年龄，并用该年龄减去研究开始时的实际年龄），则截距会产生完全不同的解释。
    以 18 岁为基准，将每位学生的年龄减去 18，那么截距将表示：对于 21 岁入学的学生，其进入研究前三年前（即 18 岁）因变量的预期值。如果中心化的目的是将年龄差异作为一个重要因素来处理，那么接下来介绍的替代方法可能更为合适。
  2. 多组（multigroup）模型。关心不同组之间的差异，将组作为分组变量。可为每一组分别建立增长模型，并比较各组的截距与斜率是否相同。
    在每个队列组中分别设定潜在增长曲线模型，则可比较不同队列间的截距或斜率。根据各组中斜率因子载荷的设定方式，研究者可以使用研究的波次或队列自身的时间度量作为截距解释的参照点（Duncan, Duncan, Strycker & Chaumeton, 2007）。在大学生的例子中，如在各组中为斜率因子使用相同的载荷（如 ​\lambda_{t1} = 0, 1, 2, 3），则所有队列都将以大学第一年作为共同的参照点。另一种做法是为每个组使用不同的载荷，使共同的截距代表最早年龄时的预期值（例如：对 18 岁入学者使用 ​\lambda_{t1}=0,1,2,3；对 19 岁入学者使用 ​\lambda_{t1}=1,2,3,4；对 20 岁入学者使用 ​\lambda_{t1}=2,3,4,5；对 21 岁入学者使用 ​\lambda_{t1}=3,4,5,6）。
  3. 直接使用时间量尺，如“年龄”本身作为斜率载荷，使各队列的资料在同一个时间轴（例如年龄 18–25 岁）上结合。斜率因子的载荷由完整的年龄范围构成，通过缺失数据估计来处理那些队列之间不重叠的年龄区间。将多个通常部分重叠的队列结合起来，并使用单一时间度量的这一策略被称为“队列趋同”（cohort convergence；Estrada & Ferrer, 2019）。
    在大学年龄队列研究中，我们可以使用学生的年龄作为增长曲线载荷，其范围从 18 岁跨越到 25 岁。19 岁入学的新生在 18 岁处将全部为缺失值，而 18 岁入学的学生在 23、24 与 25 岁处将为缺失值。该策略涉及对未实际观测到的年龄进行一定程度的外推，并假设缺失数据至少可视为 MAR。

个体差异时间点

当样本间的起始与结束观测时间存在较大差异时，可使用变量定义法 来估计增长曲线（Neale et al., 2002）。该方法允许研究者依据每个个体的实际时间信息（如年龄、日历年份）对斜率因子的因子载荷进行逐个案例的指定，从而将时间度量（如年龄、年份）直接映射到载荷矩阵。例如，不同年龄进入研究的大学生，其观测点可分别链接到 0,1,2, 的载荷，从而在同一模型中实现不同个体的时间对齐。

使用更广泛时间度量（如税年）可能带来的推论问题。以跨州公司税政策为例，若以年份（2002–2011）为时间指标建模三州四年收入数据，需要对未观测年份进行理论外推；此外，不同州在不同年份被观测意味着使用横断面差异来推断纵向发展趋势，因而会混淆队列效应与长期变化。这种外推并非必然错误，但解释上需谨慎。

另一个重要限制是：若不同队列之间观测区间几乎没有重叠，数据将极其稀疏，导致模型难以估计，因为任一时间点约有三分之二以上的城市没有数据。若存在更多队列，且观测起止年份更分散，则每个时间点的缺失会减少，估计更可行，但队列与时间效应的混淆仍然存在，只是程度较低。

Example 7.5

title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.5a,
    Latent Growth Curve Models;

data: file=health.dat; format=free;

define: !categorize age to illustrate age time metric;  
   if age le 54 then agecat = 0;
   if (age gt 54 and age le 59) then agecat = 5;
   if age gt 59 then agecat = 10;
! create scores by age variables;
   if agecat eq 0 then bmi50 = bmi1;
   if agecat eq 0 then bmi52 = bmi2;
   if agecat eq 0 then bmi54 = bmi3;
   if agecat eq 0 then bmi56 = bmi4;
   if agecat eq 0 then bmi58 = bmi5;
   if agecat eq 0 then bmi60 = bmi6;
   if agecat eq 5 then bmi55 = bmi1;
   if agecat eq 5 then bmi57 = bmi2;
   if agecat eq 5 then bmi59 = bmi3;
   if agecat eq 5 then bmi61 = bmi4;
   if agecat eq 5 then bmi63 = bmi5;
   if agecat eq 5 then bmi65 = bmi6;
   if agecat eq 10 then bmi60 = bmi1;
   if agecat eq 10 then bmi62 = bmi2;
   if agecat eq 10 then bmi64 = bmi3;
   if agecat eq 10 then bmi66 = bmi4;
   if agecat eq 10 then bmi68 = bmi5;
   if agecat eq 10 then bmi70 = bmi6;

variable: 
    names=
    age 
    srh1 srh2 srh3 srh4 srh5 srh6
    bmi1 bmi2 bmi3 bmi4 bmi5 bmi6 
    cesdna1 cesdpa1 cesdso1
    cesdna2 cesdpa2 cesdso2
    cesdna3 cesdpa3 cesdso3
    cesdna4 cesdpa4 cesdso4
    cesdna5 cesdpa5 cesdso5
    cesdna6 cesdpa6 cesdso6
    diab1 diab2 diab3 diab4 diab5 diab6;

    usevariables= 
    bmi50 bmi52 bmi54 bmi56 bmi58 bmi60   
        bmi62 bmi64 bmi66 bmi68 bmi70;   
   
analysis: type=general; 
   !missing data estimation is default;

model: !growth model using age (50-70) rather than wave as basis of time;
    i by bmi50@1 bmi52@1 bmi54@1 bmi56@1 bmi58@1 bmi60@1   
        bmi62@1 bmi64@1 bmi66@1 bmi68@1 bmi70@1;
    s by bmi50@0 bmi52@2 bmi54@4 bmi56@6 bmi58@8 bmi60@10   
        bmi62@12 bmi64@14 bmi66@16 bmi68@18 bmi70@20;
    i s;
    i with s;
    [i s];
    [bmi50-bmi70@0];

output:  sampstat stdyx;

这些变量的斜率载荷为 ​\lambda_t = 0, 2, 4, \ldots, 20。因此，所估计的线性增长覆盖了 22 年时间、以两年为单位递增。截距均值被定义为一名在 50 至 <65 岁年龄组开始研究的受试者的预期 BMI 值。值得注意的是，按照这种时间度量，只有大约三分之一的受试者在第一个时间点具有观测值，因此必须使用 FIML 方法处理缺失数据。模型拟合指标满足良好拟合的推荐标准：​\chi^2(36)=485.674, \text{CFI}=.986, \text{SRMR}=.068, \text{RMSEA}=.048。截距平均值为 27.019，表示若个体在 50 至 <55 岁开始研究，其预期 BMI 值为约 27.0。斜率估计为 .083（​p<.05），表明 BMI 每年约增加该数值。该斜率估计值大约是示例 7.3 中控制年龄、使用双年波次时间度量所得估计值的一半。标准化斜率估计为 .387，与使用波次时间编码并控制年龄时所得的标准化斜率估计非常接近。年龄度量模型的方差与条件模型差异更明显：截距因子方差为 25.113，斜率因子方差为 .046。

title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.5b,
    Latent Growth Curve Models;

data: file=health.dat; format=free;

define: !categorize age to illustrate age time metric;  
   if age le 54 then agecat = 0;
   if (age gt 54 and age le 59) then agecat = 1;
   if age gt 59 then agecat = 2;
! create individually varying time scores based on 3 categories;
   if agecat eq 0 then a1 = 0;
   if agecat eq 0 then a2 = 2;
   if agecat eq 0 then a3 = 4;
   if agecat eq 0 then a4 = 6;
   if agecat eq 0 then a5 = 8;
   if agecat eq 0 then a6 = 10;
   if agecat eq 1 then a1 = 5;
   if agecat eq 1 then a2 = 7;
   if agecat eq 1 then a3 = 9;
   if agecat eq 1 then a4 = 11;
   if agecat eq 1 then a5 = 13;
   if agecat eq 1 then a6 = 15;
   if agecat eq 2 then a1 = 10;
   if agecat eq 2 then a2 = 12;
   if agecat eq 2 then a3 = 14;
   if agecat eq 2 then a4 = 16;
   if agecat eq 2 then a5 = 18;
   if agecat eq 2 then a6 = 20;

variable: 
    names=
    age 
    srh1 srh2 srh3 srh4 srh5 srh6
    bmi1 bmi2 bmi3 bmi4 bmi5 bmi6 
    cesdna1 cesdpa1 cesdso1
    cesdna2 cesdpa2 cesdso2
    cesdna3 cesdpa3 cesdso3
    cesdna4 cesdpa4 cesdso4
    cesdna5 cesdpa5 cesdso5
    cesdna6 cesdpa6 cesdso6
    diab1 diab2 diab3 diab4 diab5 diab6;

    usevariables= 
    bmi1 bmi2 bmi3 bmi4 bmi5 bmi6 a1-a6;   
  
    tscores = a1-a6;  
   
analysis: type=random; !required for individually time varying scores;

model: !growth model with individually varying time scores; 
! Mplus short cuts required for individually varying tscores;
    i s | bmi1-bmi6 at a1-a6;
    i s;
    i with s;

output:  sampstat;

https://www.longitudinalsem.com/lsem2/ex7-5a.R

为三个年龄组分别创建时间分数变量，其起始点相差五年，并以两年为单位递增。具体如下：年龄 50–54 的时间分数为 t=0,2,4,6,8,10；年龄 55–59 的时间分数为 t=5,7,9,11,13,15；年龄 ≥60 的时间分数为 t=10,12,14,16,18,20。所有时间分数的完整范围为 0,2,4,…,200。此方法中，研究者可直接使用年龄，仅需将时间变量与斜率因子载荷矩阵相连接，但在许多应用中，更偏好通过重新缩放年龄，使第一年龄点的值为 0。由于此估计方法不提供传统的模型拟合信息，因此无法报告相应指标。在该方法下，截距平均估计为 26.948，斜率平均估计为 .073（p<.001）。斜率值与前一模型采用年龄评分方法所得的结果相近。截距与斜率方差均显著，且与年龄编码模型高度相似：截距方差为 24.773（p<.001），斜率方差为 .048（p<.001）。

二阶 LGCM：各时点的多指标测量

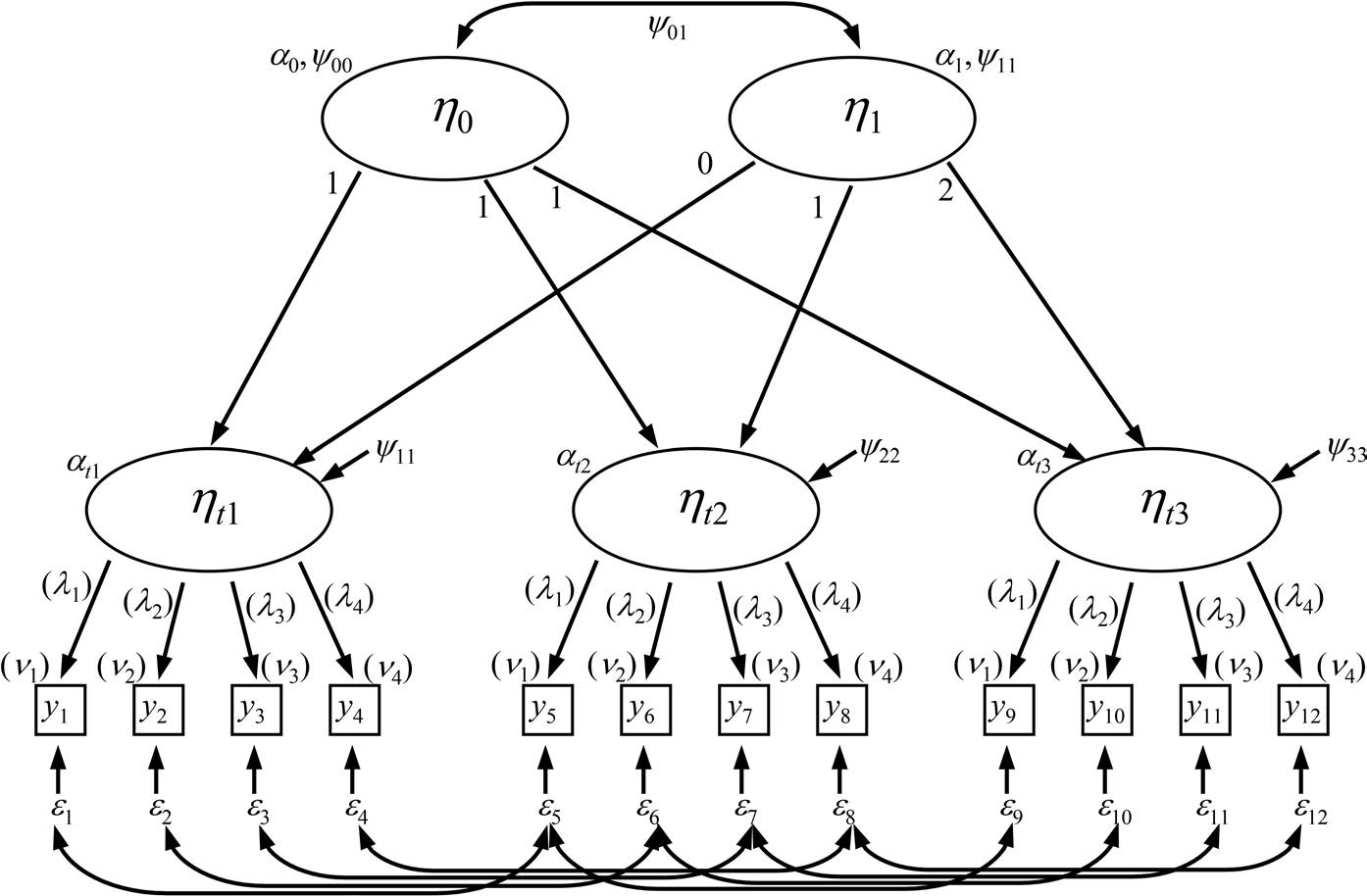
潜在增长曲线模型可以扩展为在每个时间点包含多重指标的形式。二阶的截距与斜率因子的载荷设定与一阶增长模型完全平行：截距因子的所有载荷均为 1，斜率因子的载荷按照选定的时间指标设置（如 ​\beta_{t1} = 0, 1, 2, …）。

为了让一阶因子的均值完全由其测量尺度决定，通常将一阶因子回归到二阶增长因子的回归截距（图中 ​\alpha_{t1}）设为 0。若需要，也可以在一阶干扰项 ​\psi_{tt} 上施加“跨时间等方差”的约束，并用卡方差异检验比较。

与其他具有多指标的纵向结构模型一致，在二阶增长曲线模型中一般会例行地加入测量残差的相关。对每个重复指标随时间加入相关，能够产生更准确的截距与斜率协方差估计，并总体上获得更好的模型拟合（Murphy, Beretvas & Pituch, 2011）。测量残差的相关结构可能因可用的时间点数量而呈现不同形式，可依据理论先验或经验基础确定。常见结构包括跨所有时间点的重复指标相关、滞后 1 结构，或其他替代结构（例如一阶 simplex）。时间点较少时，可用的误差结构选择也更少。在自由度允许的前提下，可以使用嵌套模型检验比较这些结构的拟合。另一种方式是使用方法因子，做法与第 6 章状态-特质误差模型中的策略类似。

一阶因子的尺度

一阶因子的尺度设定会直接影响二阶增长因子的截距与斜率解释。最常见的做法是参照指标法（选一个指标固定负荷与测量截距），但不同参照指标可能得到不同的增长结果。

  • **Ferrer ****等 (2008) **的两步法：先以独立的纵向验证性因子分析估计一阶因子的均值和方差，再在增长模型中将某一载荷固定为该估计值，以识别二阶增长模型。
  • 效应编码法：通过对载荷与测量截距施加效应编码约束，使所有指标共同决定一阶因子的尺度，从而提供最理想、最稳定的尺度设定。
  • 简单替代方案：在软件无法支持复杂约束时，可将所有载荷设为 1、所有测量截距设为 0，虽然可能降低拟合度，但仍能使所有指标共同贡献因子均值与方差。
  • 加权平均方案：利用初步纵向验证性因子分析得到的因子分数，将因子均值识别为观测指标的加权平均，从而替代等权重或参照指标设定的方法。

二分类与有序观测变量

当指标为二分或有序变量时，二阶因子模型可在采用分类 MLR 或 WLSMV 进行适当估计的前提下进行检验。在此之前，应进行因子载荷与测量阈值的等值性检验。此类检验需注意若干特殊事项（第 2 章将更详细地讨论二分与有序变量的等值性检验问题）。Liu 与 West（2018）的研究表明，需要保持等值性的不仅是载荷与阈值。他们指出，截距与斜率方差会受到一阶有序指标的测量残差非等值性的影响，并在使用一阶有序指标的二阶增长曲线模型情境中阐释了等值性问题。Winter 与 Depaoli（2022）展示了二阶增长曲线模型中的近似等值性方法。Wang 及其同事（Wang, Kohli & Henn, 2016）探讨了使用二分与有序指标的二阶增长模型中涉及 IRT 概念的相关问题。

二阶增长曲线模型的优势

二阶模型不会改变平均截距与平均斜率（均值不受测量误差影响），但主要优势在于提高信度：测量误差被分离出去，时间点特定方差由一阶因子干扰项表示，从而减少 occasion-specific variance，提高斜率与截距的信度并提升统计检验力。

在每个时间点观测方差会被分解为测量残差方差（误差与特异方差）和因子方差（真实分数方差），即​\text{Var}(y_{j}) = \lambda_{ij}^2 \psi_{jj} + \text{Var}(\varepsilon_{(j)}),在二阶增长曲线模型中，测量残差方差 ​\text{Var}(\varepsilon_{(j)}) = \theta_{(tt)} 不再代表时点特定的变异。相反，与一阶因子相关的扰动方差 ​\psi_{(tt)} 才代表时点特定方差。该减少的时点特定方差会提高信度估计。例如，以 Raudenbush 和 Bryk (2002) 的信度公式 ​\rho_{RB} 为例，将测量残差方差替换为因子扰动方差，可得：​\rho_1 = \frac{\psi_{11}}{\psi_{11} + \psi_{(t)}/T}.此处的值可以来自施加等值约束的模型，或为扰动方差估计的平均值。

由于测量残差方差通常大于 0，因此二阶模型中利用因子扰动而得到的时点特定变异会小于一阶模型中基于残差方差得到的值。结果便是斜率信度的估计得到改善，从而对标准误估计与统计效力有益。直观地看，如果某观测包含测量误差，则在各时点上其观测值偏离预测值的程度会更大；因此去除测量误差后，斜率估计会更精确。同理，截距的估计精度也会因二阶模型的应用而提高，并可据此修正其信度估计。

二阶潜在增长曲线模型的另一优势在于能够纳入自相关测量残差，以计入稳定的特异方差。一阶增长曲线模型无法估计特异方差的自相关，因此在存在真实自相关时会产生偏差。测量残差的自相关属于协方差结构而非均值结构，因此其最主要的影响表现为：改变截距与斜率的协方差、改变时点特定方差（即因子扰动）。两个时间点的重复测量的协方差如何部分由测量残差的协方差解释：

\operatorname{Cov}(y_j, y_{j^\circ}) = \psi_{00} + \lambda_{j1} \lambda_{j^\circ 1}, \psi_{11} + \lambda_{j1}, \psi_{01} + \lambda_{j^\circ 1}, \psi_{01} + \operatorname{Cov}(\varepsilon_j, \varepsilon_{j^\circ}).

在将观测协方差分解为这些组成部分后可以看出：若测量残差的自协方差不为 0，则因子方差与协方差参数必然需要相应调整；并且若真实自相关大于 0，将这些元素纳入模型之后模型拟合也会有所改善。

二阶增长曲线模型当然也能包含时间不变或 TVC，其注意事项与一阶模型几乎相同。在二阶增长曲线模型中，TVC 会预测时点特定的潜在因子而不是观测变量。同样地，关于群体差异的分析也可通过 MIMIC 模型或多组模型延伸至二阶增长曲线的情境。

Example 7.6:

https://www.longitudinalsem.com/lsem2/ex7-6a.inp

https://www.longitudinalsem.com/lsem2/ex7-6b.inp

https://www.longitudinalsem.com/lsem2/ex7-6c.inp

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.6a
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", _header_=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

library(lavaan)
#second order latent growth curve model;
#equality constraints on loading and intercepts omitted for this example;
model7.6a <- '  
  #first loading is referent by default;
    eta1 =~ cesdna1 + cesdpa1 + cesdso1
    eta2 =~ cesdna2 + cesdpa2 + cesdso2
    eta3 =~ cesdna3 + cesdpa3 + cesdso3
    eta4 =~ cesdna4 + cesdpa4 + cesdso4
    eta5 =~ cesdna5 + cesdpa5 + cesdso5
    eta6 =~ cesdna6 + cesdpa6 + cesdso6

  #set first measurement intercept to 0
    cesdna1 ~ 0*1
    cesdpa1 ~ 1
    cesdso1 ~ 1
    cesdna2 ~ 0*1
    cesdpa2 ~ 1
    cesdso2 ~ 1
    cesdna3 ~ 0*1
    cesdpa3 ~ 1
    cesdso3 ~ 1
    cesdna4 ~ 0*1
    cesdpa4 ~ 1
    cesdso4 ~ 1
    cesdna5 ~ 0*1
    cesdpa5 ~ 1
    cesdso5 ~ 1
    cesdna6 ~ 0*1
    cesdpa6 ~ 1
    cesdso6 ~ 1
  
    i =~ 1*eta1 + 1*eta2 + 1*eta3 + 1*eta4 + 1*eta5 + 1*eta6
    s =~ 0*eta1 + 1*eta2 + 2*eta3 + 3*eta4 + 4*eta5 + 5*eta6
  
    i ~~ i
    s ~~ s
    i ~~ s
  
    i ~ 1
    s ~ 1
  
    #factor means set to 0
    eta1 ~ 0
    eta2 ~ 0
    eta3 ~ 0
    eta4 ~ 0
    eta5 ~ 0
    eta6 ~ 0 
'

fitmodel7.6a <- growth(model7.6a, _data_=health1)
summary(fitmodel7.6a, _fit.measures_=TRUE, _standardized_=TRUE, _rsquare_=TRUE)

初始模型采用参照指标法识别一阶因子，即在每个时间点将第一个载荷和第一个测量截距分别设定为 1 与 0。对于此模型，为了展示其与一阶模型的关系，其余载荷和测量截距未在时间上设置为相等。同时，为了使示例更为简洁，模型中也省略了测量误差项的相关性。

第二阶增长曲线模型的结果显示：截距因子均值 ​\alpha_0 为 .276，斜率因子均值 ​\alpha_1 为 .009（​p < .001）。斜率平均值的标准化估计为 .172，表明在六个波次中抑郁程度有小到中等程度的上升。截距因子均值与参照指标（消极情绪）的观测均值 .270 十分接近。截距方差为 .160（​p < .001），斜率方差为 .003（​p < .001）。

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.6b
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

health1 <- read.table ("health.dat", _header_=FALSE)
names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

library(lavaan)
#first order growth curve model with composite scores for comparison;
#model for only the first variable used as an indicator in the second-order model;
model7.6b <- '  
    i =~ 1*cesdna1 + 1*cesdna2 + 1*cesdna3 + 1*cesdna4 + 1*cesdna5 + 1*cesdna6
    s =~ 0*cesdna1 + 1*cesdna2 + 2*cesdna3 + 3*cesdna4 + 4*cesdna5 + 5*cesdna6

    i ~~ i
    s ~~ s
    i ~~ s
  
    i ~ 1
    s ~ 1
  
    cesdna1 ~ 0*1
    cesdna2 ~ 0*1
    cesdna3 ~ 0*1
    cesdna4 ~ 0*1
    cesdna5 ~ 0*1
    cesdna6 ~ 0*1 
'

fitmodel7.6b <- growth(model7.6b, _data_=health1)
summary(fitmodel7.6b, _fit.measures_=TRUE, _standardized_=TRUE, _rsquare_=TRUE)

为了比较，对仅包含参照指标（消极情绪）的一阶潜在增长曲线模型进行了检验。该模型的截距因子均值为 .276，斜率因子均值为 .009（​p < .001），与使用三个指标的二阶模型完全一致。截距方差为 .156（​p < .001），斜率方差为 .003（​p < .001），与二阶模型相同或几乎相同。一阶与二阶模型的标准误与显著性检验结果也高度一致。例如，斜率因子均值的 Wald 比值在二阶模型中为 5.203，在一阶模型中为 5.171。

#title:  Newsom Longitudinal SEM2 Chapter 7, Example 7.6c
cat("\014")  
library(rstudioapi)
setwd(dirname(getActiveDocumentContext()$path))

names(health1) = c("age", "srh1", "srh2", "srh3", "srh4", "srh5", "srh6", "bmi1",
"bmi2", "bmi3", "bmi4", "bmi5", "bmi6", "cesdna1", "cesdpa1", "cesdso1",
"cesdna2", "cesdpa2", "cesdso2", "cesdna3", "cesdpa3", "cesdso3",
"cesdna4", "cesdpa4", "cesdso4", "cesdna5", "cesdpa5", "cesdso5",
"cesdna6", "cesdpa6", "cesdso6", "diab1", "diab2", "diab3 ", "diab4", "diab5", "diab6")

library(lavaan)
#second order growth curve model with effects coding scaling of 1st order factors;
#free first loading with NA* to remove default 1st item referent;
#use of the same labels across waves sets equality constraints on loadings and intercepts;
model7.6c <- '  #first loading is referent by default;
    #equality constraints on loading and intercepts omit for this example;

    eta1 =~ NA*cesdna1 + (lambda1)*cesdna1 + (lambda2)*cesdpa1 + (lambda3)*cesdso1
    eta2 =~ NA*cesdna2 + (lambda1)*cesdna2 + (lambda2)*cesdpa2 + (lambda3)*cesdso2
    eta3 =~ NA*cesdna3 + (lambda1)*cesdna3 + (lambda2)*cesdpa3 + (lambda3)*cesdso3
    eta4 =~ NA*cesdna4 + (lambda1)*cesdna4 + (lambda2)*cesdpa4 + (lambda3)*cesdso4
    eta5 =~ NA*cesdna5 + (lambda1)*cesdna5 + (lambda2)*cesdpa5 + (lambda3)*cesdso5
    eta6 =~ NA*cesdna6 + (lambda1)*cesdna6 + (lambda2)*cesdpa6 + (lambda3)*cesdso6

    cesdna1 ~ (nu1)*1
    cesdpa1 ~ (nu2)*1
    cesdso1 ~ (nu3)*1
    cesdna2 ~ (nu1)*1
    cesdpa2 ~ (nu2)*1
    cesdso2 ~ (nu3)*1
    cesdna3 ~ (nu1)*1
    cesdpa3 ~ (nu2)*1
    cesdso3 ~ (nu3)*1
    cesdna4 ~ (nu1)*1
    cesdpa4 ~ (nu2)*1
    cesdso4 ~ (nu3)*1
    cesdna5 ~ (nu1)*1
    cesdpa5 ~ (nu2)*1
    cesdso5 ~ (nu3)*1
    cesdna6 ~ (nu1)*1
    cesdpa6 ~ (nu2)*1
    cesdso6 ~ (nu3)*1
  
    cesdna1 ~~ cesdna2 + cesdna3 + cesdna4 + cesdna5 + cesdna6
    cesdna2 ~~ cesdna3 + cesdna4 + cesdna5 + cesdna6
    cesdna3 ~~ cesdna4 + cesdna5 + cesdna6
    cesdna4 ~~ cesdna5 + cesdna6
    cesdna5 ~~ cesdna6
    cesdpa1 ~~ cesdpa2 + cesdpa3 + cesdpa4 + cesdpa5 + cesdpa6
    cesdpa2 ~~ cesdpa3 + cesdpa4 + cesdpa5 + cesdpa6
    cesdpa3 ~~ cesdpa4 + cesdpa5 + cesdpa6
    cesdpa4 ~~ cesdpa5 + cesdpa6
    cesdpa5 ~~ cesdpa6
    cesdso1 ~~ cesdso2 + cesdso3 + cesdso4 + cesdso5 + cesdso6
    cesdso2 ~~ cesdso3 + cesdso4 + cesdso5 + cesdso6
    cesdso3 ~~ cesdso4 + cesdso5 + cesdso6
    cesdso4 ~~ cesdso5 + cesdso6
    cesdso5 ~~ cesdso6
  
  
    i =~ 1*eta1 + 1*eta2 + 1*eta3 + 1*eta4 + 1*eta5 + 1*eta6
    s =~ 0*eta1 + 1*eta2 + 2*eta3 + 3*eta4 + 4*eta5 + 5*eta6
  
    i ~~ i
    s ~~ s
    i ~~ s
  
    i ~ 1
    s ~ 1
  
    eta1 ~ 0*1
    eta2 ~ 0*1
    eta3 ~ 0*1
    eta4 ~ 0*1
    eta5 ~ 0*1
    eta6 ~ 0*1 
  
    #model constraints;
    lambda1 == 3 - lambda2 - lambda1
    (nu1) == 0 - (nu2) - (nu3) '

fitmodel7.6c <- growth(model7.6c, _data_=health1)
summary(fitmodel7.6c, _fit.measures_=TRUE, _standardized_=TRUE, _rsquare_=TRUE)

最后，为展示更优的模型设定，对二阶潜在增长曲线模型施加影响编码缩放约束的方式进行了检验。影响编码缩放会基于每次测量的指标加权平均值来生成增长模型估计，使其更能代表一阶因子的真实指标。该模型包括跨时间的载荷与测量截距相等约束，以及重复测量指标的残差相关。截距与斜率因子的时间载荷采用标准时间分数，即 ​\lambda_{t1} = 0, 1, 2, 3, 4, 5。根据替代拟合指标，该模型拟合良好，​\chi^2(111)=815.215,\ \text{CFI}=.981,\ \text{SRMR}=.045,\ \text{RMSEA}=.034。

截距因子均值为 .301，斜率因子均值为 .005（​p < .001），表明研究六个波次中抑郁程度呈上升趋势。斜率因子均值的标准化估计为 .119（相比参照指标缩放方法所得值 .172），依然提示抑郁随时间略有增加。截距与斜率方差分别为 .096 与 .002，二者均在 ​p < .001 水平显著。

斜率的信度使用 ​ρ_{RB} 公式、以平均扰动方差计算为：

\rho = \frac{\psi_{11}}{\psi_{11} + \psi_{tt}/T} = \frac{.002}{.002 + .089/6} = .119.

尽管不同缩放约束下模型结论并无实质差异，但三种模型的结果仍略有不同。对于其他数据集与变量，缩放约束的选择可能会对结论产生更大的影响。

统计检验力，时间点和样本量

这一节提供了关于潜在增长曲线模型的样本量、时间点数量与统计检验力的简要说明。

一般的 SEM 样本量建议（如至少 100 个样本，或每个测量指标 5–10 个样本）常用于增长模型，但这些建议十分粗略。模型复杂度、缺失、变量类型、估计方法（ML、WLSMV、Bayesian）都会影响收敛与检验力。

线性增长模型至少需要三个时间点，但只有三个时间点时收敛问题常见（Fan & Fan, 2005）。五个或更多时间点时，即使只有 50–100 个样本通常也能稳定收敛。若包含残差相关结构，收敛与估计都会改善，尤其当时间点多（如八个）时。

二分类指标的增长模型需要更多样本。三时间点的情形至少需要 1,000 个样本才能确保收敛；五时间点约需 500 个样本；七时间点约需 200 个样本。MLR 在小样本时通常比 WLSMV 更能收敛。

Bayesian 在小样本下可能效果更好（20–50 个样本也可能可用），但严重依赖良好的先验；非信息性先验在小样本时表现很差。

检验力需区分“固定效应”（平均截距、平均斜率）与“随机效应”（截距与斜率的方差）。测试固定效应需要的样本较少：约 50 个样本 × 五个时间点即可。增长曲线的模拟研究一般建议 50–75 个样本可检测中等效应；100 个样本可检测较小效应。测试斜率方差需要更多样本，因为随机效应用于解释个体间差异。根据 Muthén & Curran（1997），要检测斜率方差的小效应需约 500 个样本 × 五个时间点。其他研究也支持这一点。

Rast 和 Hofer（2014）对不同研究的分析显示，要检测小的斜率方差时，三时间点需要 >3,000 样本，四时间点约 1,800 样本，五时间点约 750 样本。间隔越大、时间点越多，所需样本越少。对于二分类指标，三时间点或 100 个样本会严重偏误，应避免。五时间点加 200 个样本可得到合理的方差估计。

检测协变量效应（即斜率的跨层交互）或两个斜率之间的相关需要更多样本，比检测斜率方差所需样本更大。例如，二分类协变量的“交叉斜率”（disordinal interaction）效应检验尤其低检验力，检测中等效应需约 300 个样本。

二阶增长模型（多指标）可显著提高检验力，因为测量误差被分离后，斜率的信度更高。研究显示，高负荷的一阶指标会使检测协变量效应所需的样本量减少近一半；二阶模型比一阶模型在检测斜率与截距方差时更精准，也更敏感。

总体而言，三到四个时间点与至少 100 个样本可检测中等效应的固定效应；随机效应与交互效应需要更多样本，可能需几百个。多个指标可降低样本需求，提高探测小效应的能力。最终，研究规划不应只依赖一般模拟研究，而需根据目标效应大小进行专门的检验力分析。

拓展

多组模型（Multigroup Models）

多组增长曲线模型特别适合分析典型的纵向设计——例如队列序列设计。多组 SEM 允许在不同已知组别（如政治立场、居住国家或婚姻状态）之间比较截距与斜率的均值与方差，并可灵活设定不同的误差结构。若需要更探索性的分组，可用潜类别模型根据个体的初始水平与增长率进行分组（详见第 11 章）。

纳入自回归结构（Incorporating Autoregressive Effects）

增长曲线模型可以加入自回归效应，形成“自回归潜在轨迹模型”（autoregressive latent trajectory model），其目的在于移除测量点之间的自回归成分，使趋势估计不受其干扰。也可只在残差之间设定自回归路径（structured residuals）。这两者在某些条件下是等价的，但直接在观测变量之间加入自回归路径会改变截距与斜率因子的含义，而且会与增长成分产生冗余。残差层面的自回归不会造成这种重复，但这两类模型都可能遮蔽非线性或异质性，并需要至少五个时间点才能估计。

将增长曲线纳入更复杂的模型（Incorporation of Growth Curves into Larger Models）

由于增长曲线模型属于 SEM 框架，它可以扩展为更复杂的结构。例如，斜率与截距因子不仅能被预测，也能作为预测变量去预测其他潜变量。这为研究随时间变化的影响机制提供了丰富的建模可能性，然而现实研究仍然较少充分利用这种灵活性。

平行过程增长曲线（Parallel Process Growth Curves）

平行过程模型允许同时估计多个变量的增长轨迹，并考察它们的增长是否相互对应。通常会估计两个截距、两个斜率，以及它们之间的协方差。有些研究会加入斜率之间的预测路径，但这种斜率 → 斜率的路径无法判定时间顺序，因为“x 的变化预测 y 的变化”与“y 的变化预测 x 的变化”会产生相同的统计结果。

中介模型（Mediation）

增长因子（截距或斜率）可以作为预测变量、中介或结果变量进入中介分析。潜在增长模型可用于探讨动态变化如何在中介过程中发挥作用。然而，与平行过程模型一样，使用增长因子并不能自动提供因果上的时间先后信息，因为不同方向的变化路径可能产生相同的模型拟合。不过，模型拟合程度有时可用于排除某些不合适的变量顺序设定。

本文来自 Newsom, J. T. (2023). Longitudinal Structural Equation Modeling: A Comprehensive Introduction (2nd ed.). Routledge. https://www.taylorfrancis.com/books/9781003263036

不清晰的地方可以自行查看原文。

内容部分可能翻译有误，请谅解。

#Quantitative Psychology 2 #SEM 1
Type I-III 平方和
使用VSCode集成R与Mplus的使用